Question

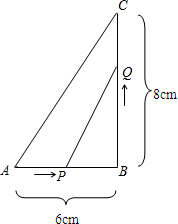
如图△ABC中，边BC=60，高AD=40，EFGH是内接矩形，HG交AD于P，设HE=x，
（1）求矩形EFGH的周长y与x的函数关系式；
（2）求矩形EFGH的面积S与x的函数关系式．

Answer 1

分析：（1）根据矩形的性质得到HG∥BC，PD=x，AP=AD-x=40-x，再三角形三角形相似的判定得到△AHG∽△ABC，利用相似比可表示出HG=

3

2

（40-x），然后根据矩形的周长确定y与x的关系；
（2）根据矩形的面积公式求解．

解答：解：（1）∵AD⊥BC，四边形EFGH是矩形，
∴HG∥BC，PD=x，AP=AD-x=40-x，
∴△AHG∽△ABC，
∴

AP

AD

=

HG

BC

，即

40-x

40

=

HG

60

∴HG=

3

2

（40-x），
∴y=2HE+2HG=2x+2×

3

2

（40-x）=2x+120-3x=120-x（0＜x＜40）；

（2）S=HE•HG=x•

3

2

（40-x）=-

3

2

x²+60x（0＜x＜40）．

点评：本题考查了相似三角形的判定与性质：平行于三角形一边的直线与其他两边所截得的三角形与原三角形相似；相似三角形对应角相等，对应边的比相等．也考查了矩形得性质．