题目内容
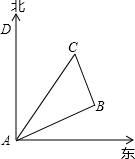 如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了500
如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了500 m到达B点,然后再沿北偏西30°方向走了500m到达目的地C点.
m到达B点,然后再沿北偏西30°方向走了500m到达目的地C点.
(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的什么方向?
解:(1)过B点作BE∥AD,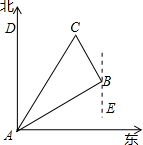
如图,∴∠DAB=∠ABE=60°.
∵30°+∠CBA+∠ABE=180°,∴∠CBA=90°.
即△ABC为直角三角形.
由已知可得:BC=500 m,AB=500 m,
m,
由勾股定理可得:AC2=BC2+AB2,
所以AC=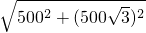 =1 000(m);
=1 000(m);
(2)在Rt△ABC中,∵BC=500 m,AC=1 000 m,
∴∠CAB=30°,∵∠DAB=60°,∴∠DAC=30°.
即点C在点A的北偏东30°的方向.
分析:(1)根据所走的方向可判断出△ABC是直角三角形,根据勾股定理可求出解.
(2)求出∠DAC的度数,即可求出方向.
点评:本题考查勾股定理的应用,先确定是直角三角形后,根据各边长,用勾股定理可求出AC的长,且求出∠DAC的度数,进而可求出点C在点A的什么方向上.

如图,∴∠DAB=∠ABE=60°.
∵30°+∠CBA+∠ABE=180°,∴∠CBA=90°.
即△ABC为直角三角形.
由已知可得:BC=500 m,AB=500
 m,
m,由勾股定理可得:AC2=BC2+AB2,
所以AC=
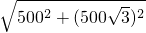 =1 000(m);
=1 000(m);(2)在Rt△ABC中,∵BC=500 m,AC=1 000 m,
∴∠CAB=30°,∵∠DAB=60°,∴∠DAC=30°.
即点C在点A的北偏东30°的方向.
分析:(1)根据所走的方向可判断出△ABC是直角三角形,根据勾股定理可求出解.
(2)求出∠DAC的度数,即可求出方向.
点评:本题考查勾股定理的应用,先确定是直角三角形后,根据各边长,用勾股定理可求出AC的长,且求出∠DAC的度数,进而可求出点C在点A的什么方向上.

练习册系列答案
相关题目
 m,出手后的铅球沿一段抛物线弧运行,当运行
m,出手后的铅球沿一段抛物线弧运行,当运行 到高度y=3m时,水平距离是x=4m.
到高度y=3m时,水平距离是x=4m. 如图,在⊙M中,
如图,在⊙M中, 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系. 如图:已知四边形ABCD和四边形ECGF都是正方形,连接BG、DE.
如图:已知四边形ABCD和四边形ECGF都是正方形,连接BG、DE.
 的解是________.
的解是________.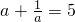 ,试求
,试求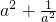 的值.
的值.