题目内容
在公式(a+b)2=a2+2ab+b2中,如果我们把a+b,a2+b2,ab分别看做一个整体,那么只要知道其中两项的值,就可以求出第三项的值.
(1)已知a+b=6,ab=-27,求a2+b2的值;
(2)已知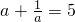 ,试求
,试求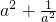 的值.
的值.
解:(1)∵a+b=6,
∴(a+b)2=36,
即a2+2ab+b2=36,
∵ab=-27,
∴a2+b2=36+2×27=90;
(2)∵a+ =5,
=5,
∴(a+ )2=25,
)2=25,
即a2+2+ =25,
=25,
∴a2+ =25-2=23.
=25-2=23.
故答案为:(1)90,(2)23.
分析:(1)把a+b=6两边平方,利用完全平方公式展开,再把ab=-27代入计算即可求解;
(2)把a+ =5两边平方,利用完全平方公式展开,整理即可求解.
=5两边平方,利用完全平方公式展开,整理即可求解.
点评:本题考查了完全平方公式的应用,熟记公式结构是解题的关键,注意整体思想的利用是解题更加简便,(2)中乘积二倍项不含字母是解题的关键.
∴(a+b)2=36,
即a2+2ab+b2=36,
∵ab=-27,
∴a2+b2=36+2×27=90;
(2)∵a+
 =5,
=5,∴(a+
 )2=25,
)2=25,即a2+2+
 =25,
=25,∴a2+
 =25-2=23.
=25-2=23.故答案为:(1)90,(2)23.
分析:(1)把a+b=6两边平方,利用完全平方公式展开,再把ab=-27代入计算即可求解;
(2)把a+
 =5两边平方,利用完全平方公式展开,整理即可求解.
=5两边平方,利用完全平方公式展开,整理即可求解.点评:本题考查了完全平方公式的应用,熟记公式结构是解题的关键,注意整体思想的利用是解题更加简便,(2)中乘积二倍项不含字母是解题的关键.

练习册系列答案
相关题目
在公式
=
+
中,(r1+r2≠0),用r1、r2表示R是( )
| 1 |
| R |
| 1 |
| r1 |
| 1 |
| r2 |
| A、R=r1+r2 | ||||
| B、R=r1r2 | ||||
C、
| ||||
D、R=
|