题目内容
16.在Rt△ABC中,∠C=90°,AC=3,BC=4,点I、O分别是△ABC的内心和外心,则tan∠IOA=2.分析 由勾股定理求出AB,得出△ABC的外接圆半径OA=$\frac{1}{2}$AB=2.5,作ID⊥AC于D,TE⊥AB于E,则ID=IE=CD=△ABC内切圆的半径=1,由切线长定理得出AE=AD=2,求出OE的长,tan∠IOA=$\frac{IE}{OE}$,即可得出结果.
解答 解:如图所示: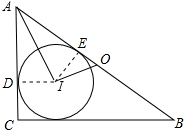
∵∠C=90°,AC=3,BC=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴OA=$\frac{1}{2}$AB=2.5,
作ID⊥AC于D,TE⊥AB于E,
则ID=IE=CD=△ABC内切圆的半径=$\frac{1}{2}$(3+4-5)=1,
∴AD=2,
由切线长定理得:AE=AD=2,
∴OE=OA-AE=0.5,
∴tan∠IOA=$\frac{IE}{OE}$=$\frac{1}{0.5}$=2.
故答案为:2.
点评 本题考查了三角形的外接圆于外心、内切圆与内心、勾股定理、切线长定理、三角函数等知识;本题综合性强,求出直角三角形的外接圆半径与内切圆半径是解决问题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
6.-$\frac{\sqrt{3}}{2}$的绝对值是( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
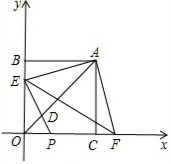 在平面直角坐标系中,点A(m,m)在第一象限,且实数m满足条件:|$\sqrt{3}$-m|=m-$\sqrt{m-4}$,AB⊥y轴于B,AC⊥x轴于C
在平面直角坐标系中,点A(m,m)在第一象限,且实数m满足条件:|$\sqrt{3}$-m|=m-$\sqrt{m-4}$,AB⊥y轴于B,AC⊥x轴于C