题目内容
8、点P（x，y）的坐标满足xy＞0，且x+y＞0，则点P在（ ）
分析：根据xy＞0，且x+y＞0，可判断xy的符号，即可确定点P所在的象限．
解答：解：∵xy＞0，
∴xy为同号即为同正或同负，
∵x+y＞0，
∴x＞0，y＞0，
∴点P（x，y）在第一象限．
故选A．
∴xy为同号即为同正或同负，
∵x+y＞0，
∴x＞0，y＞0，
∴点P（x，y）在第一象限．
故选A．
点评：坐标平面被两条坐标轴分成了四个象限，每个象限内的点的坐标符号各有特点，该知识点是中考的常考点，常与不等式、方程结合起来求一些字母的取值范围．解决本题的关键是记住平面直角坐标系中各个象限内点的符号．
练习册系列答案
相关题目
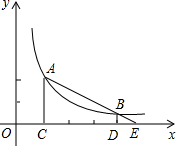如图，A、B是反比例函数
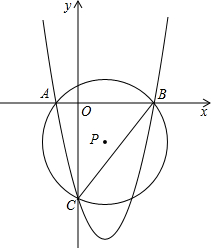已知抛物线y=x2+bx+c与y轴交于点C，与x轴交于点A（-1，0）、B（4，0），