题目内容
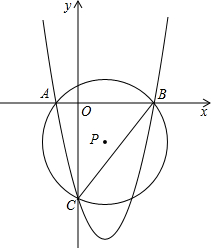 已知抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A(-1,0)、B(4,0),
已知抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A(-1,0)、B(4,0),(1)求抛物线的解析式;
(2)过点A、B、C三点作⊙P,求圆心P的坐标;
(3)在第四象限内有一点Q,若以点C、B、Q为顶点的三角形与△ABC相似,求点Q的坐标.
分析:(1)把点A、B的坐标代入抛物线解析式,利用待定系数法求二次函数解析式解答;
(2)根据垂径定理求出圆心P的横坐标为1.5,设点P(1.5,y),然后求出点C的坐标,再利用勾股定理列式表示出BP2=CP2,解方程求出y的值即可得解;
(3)根据点B、C的坐标求出△OBC是等腰直角三角形,根据等腰直角三角形的性质求出∠OBC=∠OCB=45°,利用勾股定理列式求出BC,再求出AB,然后分①∠CBQ=45°时,利用相似三角形对应边成比例分BQ和AB是对应边,BQ和BC是对应边两种情况列出比例式求解即可;②∠BCQ=45°时,与①同理求出CQ的长,从而得解;③∠Q=45°时,再分∠BCQ=∠ACB时利用相似三角形对应边成比例列式求出CQ的长,过点Q作QD⊥y轴于D,根据三角形的内角和定理和平角等于180°求出∠BAC=∠DCQ,然后利用△AOC和△QDC相似,利用相似三角形对应边成比例列式求出CD、DQ,再求出OD,从而得解;∠CBQ=∠ACB时,同理可求点Q的坐标.
(2)根据垂径定理求出圆心P的横坐标为1.5,设点P(1.5,y),然后求出点C的坐标,再利用勾股定理列式表示出BP2=CP2,解方程求出y的值即可得解;
(3)根据点B、C的坐标求出△OBC是等腰直角三角形,根据等腰直角三角形的性质求出∠OBC=∠OCB=45°,利用勾股定理列式求出BC,再求出AB,然后分①∠CBQ=45°时,利用相似三角形对应边成比例分BQ和AB是对应边,BQ和BC是对应边两种情况列出比例式求解即可;②∠BCQ=45°时,与①同理求出CQ的长,从而得解;③∠Q=45°时,再分∠BCQ=∠ACB时利用相似三角形对应边成比例列式求出CQ的长,过点Q作QD⊥y轴于D,根据三角形的内角和定理和平角等于180°求出∠BAC=∠DCQ,然后利用△AOC和△QDC相似,利用相似三角形对应边成比例列式求出CD、DQ,再求出OD,从而得解;∠CBQ=∠ACB时,同理可求点Q的坐标.
解答:解:(1)∵抛物线y=x2+bx+c与x轴交于点A(-1,0)、B(4,0),
∴
,
解得
,
∴抛物线的解析式为y=x2-3x-4;
(2)由垂径定理,圆心P在AB的垂直平分线上,
∵A(-1,0),B(4,0),
∴点P的横坐标是
=1.5,
设点P(1.5,y),
令x=0,则y=-4,
∴点C的坐标为(0,-4),
∵BP2=(4-1.5)2+y2,CP2=[y-(-4)]2+1.52,
∴(4-1.5)2+y2=[y-(-4)]2+1.52,
解得y=-1.5,
∴圆心P的坐标为(1.5,-1.5);
(3)∵B(4,0),C(0,-4),
∴OB=OC=4,
∴△OBC是等腰直角三角形,
∴∠OBC=∠OCB=45°,
由勾股定理,BC=
=
=4
,
AB=4-(-1)=5,
分①∠CBQ=45°时,点Q的横坐标与点B的横坐标相同,
BQ和AB是对应边时,△ABC≌△QBC,
∴BQ=AB=5,
此时,点Q1(4,-5),
BQ和BC是对应边时,∵△ABC∽△CBQ,
∴
=
,
即
=
,
解得BQ=
,
此时,点Q2(4,-
);
②∠BCQ=45°时,点Q的纵坐标与点C的纵坐标相同,
与①同理求出CQ=5或
,
此时,点Q3(5,-4),Q4(
,-4);
③∠Q=45°时,∠BCQ=∠ACB时,
在△AOC中,AC=
=
=
,
∵△ABC∽△BQC,
∴
=
,∠ACB=∠BCQ,
即
=
,
解得QC=
,
过点Q作QD⊥y轴于D,
∵45°+∠BAC+∠ACB=180°,
45°+∠BCQ+∠DCQ=180°,
∴∠BAC=∠DCQ,
又∵∠AOC=∠QDC=90°,
∴△AOC∽△QDC,
∴
=
=
,
即
=
=
,
解得DC=
,DQ=
,
∴OD=OC+DC=4+
=
,
此时,点Q5(
,-
),
∠CBQ=∠ACB时,同理可求点Q6(
,-
),
综上所述,存在Q1(4,-5),Q2(4,-
),Q3(5,-4),Q4(
,-4),Q5(
,-
),Q6(
,-
),使以点C、B、Q为顶点的三角形与△ABC相似.
∴
|
解得
|
∴抛物线的解析式为y=x2-3x-4;
(2)由垂径定理,圆心P在AB的垂直平分线上,
∵A(-1,0),B(4,0),
∴点P的横坐标是
| -1+4 |
| 2 |
设点P(1.5,y),
令x=0,则y=-4,
∴点C的坐标为(0,-4),
∵BP2=(4-1.5)2+y2,CP2=[y-(-4)]2+1.52,
∴(4-1.5)2+y2=[y-(-4)]2+1.52,
解得y=-1.5,
∴圆心P的坐标为(1.5,-1.5);
(3)∵B(4,0),C(0,-4),
∴OB=OC=4,
∴△OBC是等腰直角三角形,
∴∠OBC=∠OCB=45°,
由勾股定理,BC=
| OB2+OC2 |
| 42+42 |
| 2 |
AB=4-(-1)=5,
分①∠CBQ=45°时,点Q的横坐标与点B的横坐标相同,
BQ和AB是对应边时,△ABC≌△QBC,
∴BQ=AB=5,
此时,点Q1(4,-5),
BQ和BC是对应边时,∵△ABC∽△CBQ,
∴
| AB |
| CB |
| BC |
| BQ |
即
| 5 | ||
4
|
4
| ||
| BQ |
解得BQ=
| 32 |
| 5 |
此时,点Q2(4,-
| 32 |
| 5 |
②∠BCQ=45°时,点Q的纵坐标与点C的纵坐标相同,
与①同理求出CQ=5或
| 32 |
| 5 |
此时,点Q3(5,-4),Q4(
| 32 |
| 5 |
③∠Q=45°时,∠BCQ=∠ACB时,

在△AOC中,AC=
| OA2+OC2 |
| 12+42 |
| 17 |
∵△ABC∽△BQC,
∴
| BC |
| QC |
| AC |
| BC |
即
4
| ||
| QC |
| ||
4
|
解得QC=
32
| ||
| 17 |
过点Q作QD⊥y轴于D,
∵45°+∠BAC+∠ACB=180°,
45°+∠BCQ+∠DCQ=180°,
∴∠BAC=∠DCQ,
又∵∠AOC=∠QDC=90°,
∴△AOC∽△QDC,
∴
| DC |
| OA |
| DQ |
| OC |
| CQ |
| AC |
即
| DC |
| 1 |
| DQ |
| 4 |
| ||||
|
解得DC=
| 32 |
| 17 |
| 128 |
| 17 |
∴OD=OC+DC=4+
| 32 |
| 17 |
| 100 |
| 17 |
此时,点Q5(
| 128 |
| 17 |
| 100 |
| 17 |
∠CBQ=∠ACB时,同理可求点Q6(
| 100 |
| 17 |
| 128 |
| 17 |
综上所述,存在Q1(4,-5),Q2(4,-
| 32 |
| 5 |
| 32 |
| 5 |
| 128 |
| 17 |
| 100 |
| 17 |
| 100 |
| 17 |
| 128 |
| 17 |
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,抛物线与坐标轴的交点的求法,垂径定理的应用,勾股定理的应用,相似三角形的性质,难点在于(3)要分情况讨论.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.