题目内容
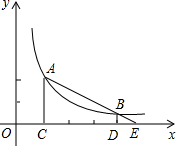 如图,A、B是反比例函数y=
如图,A、B是反比例函数y=| 2 |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据相似三角形的面积的比等于相似比的平方可知.
解答:解:∵C、D的坐标分别为(1,0),(4,0),
∴AC=2,BD=
,
∴根据相似三角形的判定可知,△BDE∽△ACE,
所以相似比是1:4,
所以△BDE的面积与△ACE的面积的比值是1:16.
故选D.
∴AC=2,BD=
| 1 |
| 2 |
∴根据相似三角形的判定可知,△BDE∽△ACE,
所以相似比是1:4,
所以△BDE的面积与△ACE的面积的比值是1:16.
故选D.
点评:主要考查了反比例函数y=
中k的几何意义和相似三角形的性质.
| k |
| x |

练习册系列答案
相关题目
 如图所示,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为3,则反比例函数的表达式是( )
如图所示,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为3,则反比例函数的表达式是( )A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
 如图,A、B是反比例函数y=
如图,A、B是反比例函数y=| k |
| x |
| A、S△ADB>S△ACB |
| B、S△ADB<S△ACB |
| C、S△ADB=S△ACB |
| D、不确定 |
 如图所示,P是反比例函数
如图所示,P是反比例函数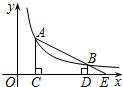 如图,A,B是反比例函数y=
如图,A,B是反比例函数y= 如图,若点P是反比例函数y=
如图,若点P是反比例函数y=