题目内容
 三角形的三条外角平分线所在直线相交构成的三角形( )
三角形的三条外角平分线所在直线相交构成的三角形( )| A、一定是锐角三角形 |
| B、一定是钝角三角形 |
| C、一定是直角三角形 |
| D、与原三角形相似 |
考点:三角形的外角性质,三角形内角和定理
专题:
分析:根据三角形的外角性质可得到:∠C′AB=
(∠ABC+∠ACB),∠C′BA=
(∠ACB+∠BAC),再根据三角形内角和定理表示出∠C′,整理可得到∠C′是锐角,同理可求得∠A′,∠B′也是锐角,从而得到△A′B′C′一定是锐角三角形.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵∠C′AB=
(∠ABC+∠ACB),∠C′BA=
(∠ACB+∠BAC),∠C′=180°-∠C′AB-∠C′BA.
∴∠C′=180°-
(∠ABC+∠ACB)-
(∠ACB+∠BAC)=90°-
∠ACB.
∵90°-
∠ACB<90°.
∴∠C′<90°.
同理:∠A′<90°,∠B′<90°.
∴△A′B′C′一定是锐角三角形.
故选A.
| 1 |
| 2 |
| 1 |
| 2 |
∴∠C′=180°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵90°-
| 1 |
| 2 |
∴∠C′<90°.
同理:∠A′<90°,∠B′<90°.
∴△A′B′C′一定是锐角三角形.
故选A.
点评:此题主要考查:(1)三角形内角和定理:三角形内角和是180°.(2)三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
 如图,D为△ABC的边BC上一点,P为线段AD上一点,若△APB的面积为9,△CPD的面积为16,则△ABC面积的最小值是
如图,D为△ABC的边BC上一点,P为线段AD上一点,若△APB的面积为9,△CPD的面积为16,则△ABC面积的最小值是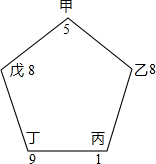 甲、乙、丙、丁、戊五名同学手拉手围成一个五边形,每个人心中想一个数,相邻的两个人把所想两数的平均数告诉与他们不相邻的那个人,结果如图所示,则乙心中所想的数是
甲、乙、丙、丁、戊五名同学手拉手围成一个五边形,每个人心中想一个数,相邻的两个人把所想两数的平均数告诉与他们不相邻的那个人,结果如图所示,则乙心中所想的数是