题目内容
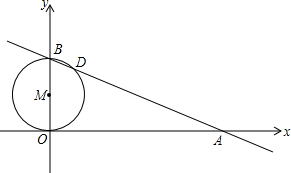
 如图,直线y=-
如图,直线y=-| 4 |
| 3 |
考点:一次函数图象上点的坐标特征,线段垂直平分线的性质,勾股定理
专题:
分析:根据直线解析式令x=0、y=0分别求出OB、OA,再根据线段垂直平分线上的点到两端点的距离相等可得AC=BC,设OC=m,利用勾股定理列出方程求出m的值,即可得到点C的坐标,再求出AC,然后根据三角形的面积公式列式计算即可得解.
解答:解:∵直线y=-
x+8,分别交x轴、y轴于A、B两点,
当x=0时,y=8,
当y=0时,x=6,
∴OA=6,OB=8,
∵CE是线段AB的垂直平分线,
∴CB=CA,
设OC=m,
则
=m+6,
解得,m=
,
∴点C的坐标为(-
,0);
∴AC=6+
=
,
∴△ABC的面积S=
AC×OB=
×
×8=
.
| 4 |
| 3 |
当x=0时,y=8,
当y=0时,x=6,
∴OA=6,OB=8,
∵CE是线段AB的垂直平分线,
∴CB=CA,
设OC=m,
则
| m2+82 |
解得,m=
| 7 |
| 3 |
∴点C的坐标为(-
| 7 |
| 3 |
∴AC=6+
| 7 |
| 3 |
| 25 |
| 3 |
∴△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 3 |
| 100 |
| 3 |
点评:本题考查了一次函数图象上点的坐标特征,线段垂直平分线上的点到两端点的距离相等的性质,勾股定理,熟记性质并列出关于OC的长度的方程是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
-2的相反数是( )
| A、-2 | B、2 |
| C、1 2? | D、12 |
 如图,直线
如图,直线