题目内容
如图,矩形OABC的两边在坐标轴上,点B的坐标为(2,4),点M是矩形对角线的交点,双曲线y= 过点M,双曲线与AB交于N,则AN:NB= .
过点M,双曲线与AB交于N,则AN:NB= .
【答案】分析:先根据四边形OABC是矩形,B(2,4)即可得出A、C两点的坐标,故可求出M点的坐标,由双曲线y= 过点M可求出k的值,进而得出反比例函数的解析式,由此可得出N点坐标,故可得出结论.
过点M可求出k的值,进而得出反比例函数的解析式,由此可得出N点坐标,故可得出结论.
解答:解:∵四边形OABC是矩形,B(2,4),
∴A(2,0)、C(0,4),
∵点M是矩形对角线的交点,
∴M(1,2),
∵双曲线y= 过点M,
过点M,
∴2=k,
∴反比例函数的解析式为y= ,
,
∴当x=2时,y=1,
∴N(2,1),
∴AN=1,NB=AB-AN=4-1=3,
∴AN:NB=1:3.
故答案为:1:3.
点评:本题考查的是反比例函数综合题,熟知矩形的特点及用待定系数法求反比例函数的解析式是解答此题的关键.
 过点M可求出k的值,进而得出反比例函数的解析式,由此可得出N点坐标,故可得出结论.
过点M可求出k的值,进而得出反比例函数的解析式,由此可得出N点坐标,故可得出结论.解答:解:∵四边形OABC是矩形,B(2,4),
∴A(2,0)、C(0,4),
∵点M是矩形对角线的交点,
∴M(1,2),
∵双曲线y=
 过点M,
过点M,∴2=k,
∴反比例函数的解析式为y=
 ,
,∴当x=2时,y=1,
∴N(2,1),
∴AN=1,NB=AB-AN=4-1=3,
∴AN:NB=1:3.
故答案为:1:3.
点评:本题考查的是反比例函数综合题,熟知矩形的特点及用待定系数法求反比例函数的解析式是解答此题的关键.

练习册系列答案
相关题目
 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
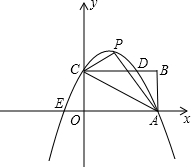 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA= (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2 如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是
如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是