题目内容
 如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是
如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是分析:在坐标系中画出函数y=x,函数将四个点所形成的矩形分成了两个部分,三角形内的点恰是满足题目要求的所有点,所以三角形与矩形的面积比即为所求概率.
解答:解 :在图中画出y=x直线,三角形内所有点恰好满足x<y,
:在图中画出y=x直线,三角形内所有点恰好满足x<y,
S△CDO=
×CD×CO=
×1×1=
,
S四边形OABC=OA•AB=4×1=4,
∴x<y的概率是:
=
=
.
故答案为:
.
 :在图中画出y=x直线,三角形内所有点恰好满足x<y,
:在图中画出y=x直线,三角形内所有点恰好满足x<y,S△CDO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S四边形OABC=OA•AB=4×1=4,
∴x<y的概率是:
| S△CDO |
| S四边形OABC |
| ||
| 4 |
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |
点评:此题主要考查了几何概率,求概率时,已知和未知与几何有关的就是几何概率.计算方法是长度比,面积比,体积比等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
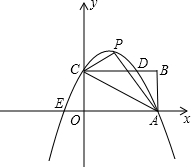 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA= (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2