题目内容
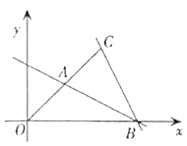
【题目】如图,平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上.
轴上.
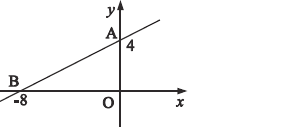
(1)求直线![]() 的解析式;
的解析式;
(2)若![]() 轴上有一点
轴上有一点![]() 使得
使得![]() 时,求
时,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() 的面积为
的面积为![]() 或
或![]()
【解析】
(1)根据点A,B的坐标,利用待定系数法可求出直线AB的解析式;
(2)设点P的坐标为(t,0),分点P在原点左侧及点P在原点右侧两种情况考虑:①若点P在x轴上原点左侧,当PB=AP时,∠APO=2∠ABO,在Rt△APO中,利用勾股定理可求出t的值,进而可得出BP的长,再利用三角形的面积公式可求出△ABP的面积;②若点P在x轴上原点右侧,由对称性,可得出点P′的坐标,进而可得出BP′的长,再利用三角形的面积公式可求出△ABP′的面积.综上,此题得解
解:(1)设直线![]() 的解析式为
的解析式为![]() ,则:
,则:
![]() 解得:
解得:![]()
∴所求直线![]() 的解析式为:
的解析式为: ![]()
(2)设点![]() 为
为![]()
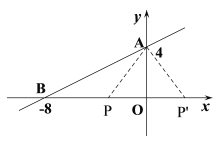
①若点![]() 在
在![]() 轴上原点左侧,当
轴上原点左侧,当![]() 时,
时,![]()
在![]() 中,
中,![]() ,
,![]() ,
,![]()
∴ ![]()
解得: ![]()
∴![]()
∴![]()
②若![]() 点在
点在![]() 轴上原点右侧,由对称性,得
轴上原点右侧,由对称性,得![]() 点为
点为![]() ,此时
,此时![]() ,
,
∴![]()
综合上述,![]() 的面积为
的面积为![]() 或
或![]() .
.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目