题目内容
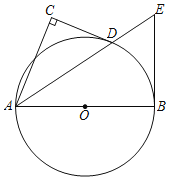
【题目】如图,已知![]() ,以
,以![]() 为直径的
为直径的![]() 交边
交边![]() 于点
于点![]() ,
,![]() 与
与![]() 相切.
相切.
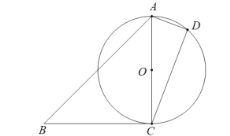
(1)若![]() ,求证:
,求证:![]() ;
;
(2)点![]() 是
是![]() 上一点,点
上一点,点![]() 两点在
两点在![]() 的异侧.若
的异侧.若![]() ,
,![]() ,
,![]() ,求
,求![]() 半径的长.
半径的长.
【答案】(1)证明见解析;(2)5
【解析】
(1)连接CE,依据题意和圆周角定理求得△ABC是等腰直角三角形,然后根据圆周角定理和等腰三角形三线合一的性质求解即可;
(2)连接DO并延长,交CE于点M,交![]() 于点G,利用三角形外角的性质求得
于点G,利用三角形外角的性质求得![]() ,从而判定DG∥AE,得到
,从而判定DG∥AE,得到![]() ,从而根据垂径定理可得EM=CM,根据三角形中位线定理可求
,从而根据垂径定理可得EM=CM,根据三角形中位线定理可求![]() ,然后设圆的半径为x,根据勾股定理列方程求解即可.
,然后设圆的半径为x,根据勾股定理列方程求解即可.
解:连接CE
∵![]() 与
与![]() 相切
相切
∴∠ACB=90°
∵![]()
∴![]()
∴CA=CB
又∵以![]() 为直径的
为直径的![]() 交边
交边![]() 于点
于点![]() ,
,
∴∠CEA=90°
∴根据等腰三角形三线合一的性质可知,CE是底边AB的中线
∴AE=BE
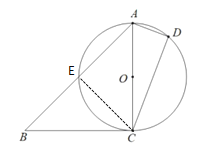
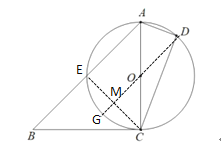
(2)连接DO并延长,交CE于点M,交![]() 于点G
于点G
由(1)可知,∠CEA=90°
∵![]()
∴DG∥AE
∴![]()
∴EM=CM
∴在△AEC中,![]()
设圆的半径为x,在Rt△OMC中,![]()
在Rt△DMC中,![]()
∴![]() ,解得
,解得![]() 或
或![]() (负值舍去)
(负值舍去)
∴![]() 半径的长为5.
半径的长为5.

练习册系列答案
相关题目