Question

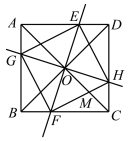
【题目】如图，已知正方形ABCD，O为对角线AC与BD的交点，过点O的直线EF与直线GH分别交AD，BC，AB，CD于点E，F，G，H，若EF⊥GH，OC与FH相交于点M，当CF=4，AG=2时，则OM的长为________．

Answer 1

【答案】

【解析】

先证明四边形是正方形，求出两个正方形的边长，得出的长度，证明，利用即可得出答案．

解：∵四边形是平行四边形，为对角线，

∴，，，

又∵

∴，，

∴

在和中，

，

∴，

∴，

，

同理可证：，

∴，

又∵，

∴四边形是正方形，

∵，，

∴，即正方形的边长为6，

在中，由勾股定理得：，

∴，

∵，

∴，

在中，由勾股定理得：，即：，

即小正方形的边长为，

∵为小正方形的对角线，

∴，

∴，

在和中，

∵，，

∴，

∴，即：，

∴，

故答案为：．