题目内容
【题目】某日,深圳高级中学(集团)南北校区初三学生参加东校区下午![]() 时的交流活动,南校区学生中午
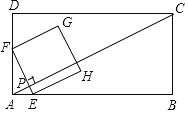
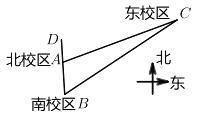
时的交流活动,南校区学生中午![]() 乘坐校车出发,沿正北方向行12公里到达北校区,然后南北校区一同前往东校区(等待时间不计).如图所示,已知东校区在南校区北偏东
乘坐校车出发,沿正北方向行12公里到达北校区,然后南北校区一同前往东校区(等待时间不计).如图所示,已知东校区在南校区北偏东![]() 方向,在北校区北偏东
方向,在北校区北偏东![]() 方向.校车行驶状态的平均速度为
方向.校车行驶状态的平均速度为![]() ,途中一共经过30个红绿灯,平均每个红绿灯等待时间为30秒.
,途中一共经过30个红绿灯,平均每个红绿灯等待时间为30秒.
(1)求北校区到东校区![]() 的距离;
的距离;
(2)通过计算,说明南北校区学生能否在![]() 前到达东校区.(本题参考数据:
前到达东校区.(本题参考数据:![]() ,
,![]() )
)
【答案】(1)![]() ;(2)能.
;(2)能.
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,然后在两个直角三角形中通过三角函数分别计算出AE、AC即可;
,然后在两个直角三角形中通过三角函数分别计算出AE、AC即可;
(2)算出总路程求出汽车行驶的时间,加上等红绿灯的时间即为总时间,即可作出判断.
解:(1)过点![]() 作
作![]() 于点
于点![]() .
.
依题意有:![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
(2)总用时为:![]() 分钟
分钟![]() 分钟,
分钟,
∴能规定时间前到达.


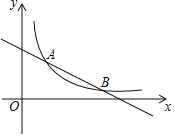
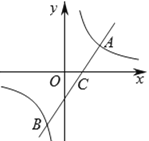
【题目】某生产商存有1200千克![]() 产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产
产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产![]() 产品,
产品,![]() 产品售价为200元/千克.经市场调研发现,
产品售价为200元/千克.经市场调研发现,![]() 产品存货的处理价格
产品存货的处理价格![]() (元/千克)与处理数量
(元/千克)与处理数量![]() (千克)满足一次函数关系(
(千克)满足一次函数关系(![]() ),且得到表中数据.
),且得到表中数据.
|
|
200 | 350 |
400 | 300 |
(1)请求出处理价格![]() (元千克)与处理数量
(元千克)与处理数量![]() (千克)之间的函数关系;
(千克)之间的函数关系;
(2)若![]() 产品生产成本为100元千克,
产品生产成本为100元千克,![]() 产品处理数量为多少千克时,生产
产品处理数量为多少千克时,生产![]() 产品数量最多,最多是多少?
产品数量最多,最多是多少?
(3)由于改进技术,![]() 产品的生产成本降低到了
产品的生产成本降低到了![]() 元/千克,设全部产品全部售出,所得总利润为
元/千克,设全部产品全部售出,所得总利润为![]() (元),若
(元),若![]() 时,满足
时,满足![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围.
的取值范围.
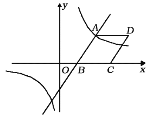
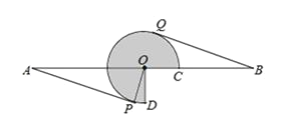
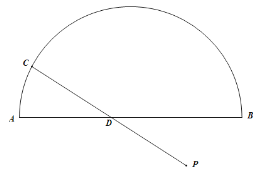
【题目】如图,![]() 是直径AB所对的半圆弧,点P是
是直径AB所对的半圆弧,点P是![]() 与直径AB所围成图形的外部的一个定点,AB=8cm,点C是
与直径AB所围成图形的外部的一个定点,AB=8cm,点C是![]() 上一动点,连接PC交AB于点D.
上一动点,连接PC交AB于点D.
小明根据学习函数的经验,对线段AD,CD,PD,进行了研究,设A,D两点间的距离为x cm,C,D两点间的距离为![]() cm,P,D两点之间的距离为
cm,P,D两点之间的距离为![]() cm.
cm.
小明根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化而变化的规律进行了探究.
随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0.00 | 1.00 | 2.00 | 3.00 | 3.20 | 4.00 | 5.00 | 6.00 | 6.50 | 7.00 | 8.00 |
| 0.00 | 1.04 | 2.09 | 3.11 | 3.30 | 4.00 | 4.41 | 3.46 | 2.50 | 1.53 | 0.00 |
| 6.24 | 5.29 | 4.35 | 3.46 | 3.30 | 2.64 | 2.00 | m | 1.80 | 2.00 | 2.65 |
补充表格;(说明:补全表格时,相关数值保留两位小数)
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点,并画出函数
中,描出补全后的表中各组数值所对应的点,并画出函数![]() 的图象:
的图象:
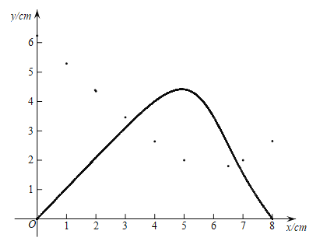
(3)结合函数图象解决问题:当AD=2PD 时,AD的长度约为___________.