题目内容
如图,∠BAC=60°,AP平分∠BAC,PD⊥AB,PE⊥AC,若AD=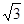 ,则PE=___.
,则PE=___.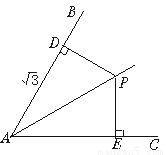
【答案】
1
【解析】
试题分析:由∠BAC=60°,AP平分∠BAC可得∠DAP=30°,即可得到AP=2DP,根据AD=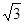 可得PD的长,再根据角平分线的性质即可求得结果.
可得PD的长,再根据角平分线的性质即可求得结果.
∵∠BAC=60°,AP平分∠BAC
∴∠DAP=30°
∵PD⊥AB
∴AP=2DP
∵AD=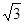
∴DP=1
∵AP平分∠BAC,PD⊥AB,PE⊥AC
∴PE=DP=1.
考点:角平分线的性质,含30°角的直角三角形的性质
点评:含30°角的直角三角形的性质是平面图形中一个非常重要的性质,在中考中比较常见,常以填空题、选择题形式出现,属于基础题,难度一般,需多加关注.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,∠BAC=60°,AP平分∠BAC,PD⊥AB,PE⊥AC,若AD=
如图,∠BAC=60°,AP平分∠BAC,PD⊥AB,PE⊥AC,若AD=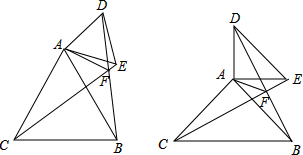 在△ABC和△ADE中,AC=AB,AE=AD,∠BAC=∠DAE=m,CE,DB交于点F,连接AF.
在△ABC和△ADE中,AC=AB,AE=AD,∠BAC=∠DAE=m,CE,DB交于点F,连接AF. 如图,∠BAC=60°,AP平分∠BAC,PD⊥AB,PE⊥AC,若AD=
如图,∠BAC=60°,AP平分∠BAC,PD⊥AB,PE⊥AC,若AD= ,则PE=________.
,则PE=________. ,则PE= .
,则PE= .