题目内容
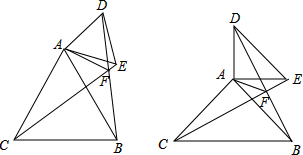 在△ABC和△ADE中,AC=AB,AE=AD,∠BAC=∠DAE=m,CE,DB交于点F,连接AF.
在△ABC和△ADE中,AC=AB,AE=AD,∠BAC=∠DAE=m,CE,DB交于点F,连接AF.(1)如图,当如图当m=60°时,猜想BD,CE的关系,并证明你的结论;
(2)在(1)的条件下,猜想线段AF,BF,CF数量关系,并证明你的结论;
(3)当m=90°时直接写出AF,BF,CF的关系.
分析:(1)由条件证明△ACE≌△ADB,就可以得出BD=CE的结论;
(2)如图1,作∠FAG=60°,交EC于点G,证明△AGC≌△AFB就可以得出结论CF=AF+BF;
(3)如图2,作GA⊥AF于点A交CF于点G,证明△AGC≌△AFB就可以得出AG=AF,△AGF是等腰直角三角形,就有GF=
AF,就可以得出结论CF=BF+
AF.
(2)如图1,作∠FAG=60°,交EC于点G,证明△AGC≌△AFB就可以得出结论CF=AF+BF;
(3)如图2,作GA⊥AF于点A交CF于点G,证明△AGC≌△AFB就可以得出AG=AF,△AGF是等腰直角三角形,就有GF=
| 2 |
| 2 |
解答:解:(1)BD=CE
理由:∵∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,
∴∠CAE=∠BAD.
在△ACE和△ADB中
,
∴△ACE≌△ADB(SAS),
∴BD=CE;
(2)CF=AF+BF
理由:如图1,作∠FAG=60°,交EC于点G.
∵∠CAB=60°,
∴∠CAB=∠GAF.
∴∠CAB-∠GAB=∠GAF-∠GAB,
即∠CAG=∠FAB.
∵△ACE≌△ADB,
∴∠ACE=∠ABD.
在△AGC和△AFB中
,
∴△AGC≌△AFB(ASA)
∴AG=AF,CG=BF.
∵∠FAG=60°,
∴△FAG为等边三角形,
∴AF=FG.
∵CF=CG+GF,
∴CF=BF+AF;
(3)CF=BF+
AF
如图2,作GA⊥AF于点A交CF于点G,
∴∠GAF=90°.
∵∠CAB=90°,
∴∠CAB=∠GAE.
∴∠CAB-∠GAB=∠GAE-∠GAB,
即∠CAG=∠FAB.
在△AGC和△AFB中
,
∴△AGC≌△AFB(ASA)
∴AG=AF,CG=BF.
∵∠FAG=90°,
∴△FAG为等腰直角三角形,
∴GF=
AF,
∵CF=CG+GF,
∴CF=BF+
AF;
理由:∵∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,
∴∠CAE=∠BAD.
在△ACE和△ADB中
|
∴△ACE≌△ADB(SAS),
∴BD=CE;
(2)CF=AF+BF
理由:如图1,作∠FAG=60°,交EC于点G.
∵∠CAB=60°,
∴∠CAB=∠GAF.
∴∠CAB-∠GAB=∠GAF-∠GAB,

即∠CAG=∠FAB.
∵△ACE≌△ADB,
∴∠ACE=∠ABD.
在△AGC和△AFB中
|
∴△AGC≌△AFB(ASA)
∴AG=AF,CG=BF.
∵∠FAG=60°,
∴△FAG为等边三角形,
∴AF=FG.
∵CF=CG+GF,
∴CF=BF+AF;
(3)CF=BF+
| 2 |
如图2,作GA⊥AF于点A交CF于点G,
∴∠GAF=90°.
∵∠CAB=90°,
∴∠CAB=∠GAE.
∴∠CAB-∠GAB=∠GAE-∠GAB,
即∠CAG=∠FAB.
在△AGC和△AFB中
|
∴△AGC≌△AFB(ASA)
∴AG=AF,CG=BF.
∵∠FAG=90°,
∴△FAG为等腰直角三角形,
∴GF=
| 2 |
∵CF=CG+GF,
∴CF=BF+
| 2 |
点评:本题考查了等边三角形的判定及性质的运用,勾股定理的运用,等腰直角三角形的运用,全等三角形的判定及性质的运用,解答时正确作出辅助线是难点,证明三角形全等是关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
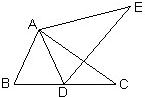 15、如图,在△ABC和△ADE中,有以下四个论断:①AB=AD,②AC=AE,③∠C=∠E,④BC=DE,请以其中三个论断为条件,余下一个论断为结论,写出一个真命题(用序号“JJJ?J”的形式写出):
15、如图,在△ABC和△ADE中,有以下四个论断:①AB=AD,②AC=AE,③∠C=∠E,④BC=DE,请以其中三个论断为条件,余下一个论断为结论,写出一个真命题(用序号“JJJ?J”的形式写出): 有一块五边形的试验田,用于种植1号良种水稻进行实验,如图所示,已知五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20米.
有一块五边形的试验田,用于种植1号良种水稻进行实验,如图所示,已知五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20米. 已知:如图所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在同一条直线上,连接BE,CD,M,N分别为BE,CD的中点,连接AM,AN,MN.
已知:如图所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在同一条直线上,连接BE,CD,M,N分别为BE,CD的中点,连接AM,AN,MN. 如图,在△ABC和△ADE中,∠DAB=∠EAC,∠C=∠E.
如图,在△ABC和△ADE中,∠DAB=∠EAC,∠C=∠E. 如图,在△ABC和△ADE中,BC、DE相交于点O,且∠C=∠E,再添加一个条件不能证明△ABC≌△ADE的是( )
如图,在△ABC和△ADE中,BC、DE相交于点O,且∠C=∠E,再添加一个条件不能证明△ABC≌△ADE的是( )