题目内容
4.若一个圆的内接正六边形的面积是24$\sqrt{3}$,则这个圆的周长是8π.分析 根据正六边形的面积,得出正六边形的半径,即可得出周长.
解答 解:设圆的半径为r,
∵圆的内接正六边形的面积是24$\sqrt{3}$,
∴$\frac{1}{2}$r•$\frac{\sqrt{3}}{2}$r×6=24$\sqrt{3}$,
解得r=4,
∴圆的周长=2π×4=8π,
故答案为8π.
点评 本题考查了正多边形和圆,利用了内接正六边形的边长与它的外接圆的半径相等求解.

练习册系列答案
相关题目
12.下列说法正确的是( )
| A. | -1不是单项式 | B. | 2πr2的次数是3 | C. | $\frac{{x}^{2}y}{3}$的次数是3 | D. | -$\frac{xy}{2}$的系数是-1 |
9.当前,“低头族”已成为热门话题之一,小颖为了了解路边行人边走路边低头看手机的情况,她应采用的收集数据的方式是( )
| A. | 对学校的同学发放问卷进行调查 | |
| B. | 对在路边行走的学生随机发放问卷进行调查 | |
| C. | 对在图书馆里看书的人发放问卷进行调查 | |
| D. | 对在路边行走的路人随机发放问卷进行调查 |
14.在直角△ABC中,AC=6,E在AC边上,满足CE=2AE,D为斜边AB的中点,F是线段BC上一动点,满足∠EDF=90°,则BF-FC的最大值是( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
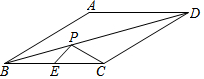 已知点E是菱形ABCD边BC上的中点,∠ABC=30°,P是对角线BD上一点,且PC+PE=$\sqrt{26}$.则菱形ABCD面积的最大值是20+8$\sqrt{3}$.
已知点E是菱形ABCD边BC上的中点,∠ABC=30°,P是对角线BD上一点,且PC+PE=$\sqrt{26}$.则菱形ABCD面积的最大值是20+8$\sqrt{3}$. 一直角三角形ABC的面积为20,在AB的同侧分别以AB、BC、CA为直径作三个半圆,求阴影部分面积.
一直角三角形ABC的面积为20,在AB的同侧分别以AB、BC、CA为直径作三个半圆,求阴影部分面积.