题目内容
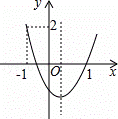
如图所示,二次函数y=﹣x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0)使S△ABD=S△ABC,求点D的坐标.
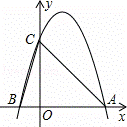
解:(1)∵二次函数y=﹣x2+2x+m的图象与x轴的一个交点为A(3,0),
∴﹣9+2×3+m=0,
解得:m=3;
(2)∵二次函数的解析式为:y=﹣x2+2x+3,
∴当y=0时,﹣x2+2x+3=0,
解得:x1=3,x2=﹣1,
∴B(﹣1,0);
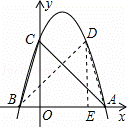
(3)如图,连接BD、AD, 过点D作DE⊥AB,
过点D作DE⊥AB,
∵当x=0时,y=3,
∴C(0,3),
若S△ABD=S△ABC,
∵D(x,y)(其中x>0,y>0),
则可得OC=DE=3,
∴当y=3时,﹣x2+2x+3=3,
解得:x=0或x=2,
∴点D的坐标为(2,3).
另法:点D与点C关于x=1对称,
故D(2,3).

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目


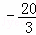 ,5),D是AB边上的一点.将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是
,5),D是AB边上的一点.将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是
 D.
D. 
 (2)中的数轴补充完整,然后用圆规在数轴上表示实数
(2)中的数轴补充完整,然后用圆规在数轴上表示实数 .
.