题目内容
如图，⊙O的直径是AB，∠C=35°，则∠DAB的度数是
- A.60°
- B.55°
- C.50°
- D.45°
B
分析：先根据圆周角定理求出∠ADB及∠C的度数，再由三角形内角和定理即可求出∠DAB的度数．
解答：∵AB是⊙O的直径，
∴∠ADB=90°，
∵∠C与∠B是
所对的圆周角，∠C=35°，
∴∠B=∠C=35°，
∴∠DAB=180°-∠ADB-∠B=180°-90°-35°=55°．
故选B．
点评：本题考查的是圆周角定理，在解答此类题目时往往用到三角形的内角和是180°这一隐藏条件．
分析：先根据圆周角定理求出∠ADB及∠C的度数，再由三角形内角和定理即可求出∠DAB的度数．
解答：∵AB是⊙O的直径，
∴∠ADB=90°，
∵∠C与∠B是
所对的圆周角，∠C=35°，∴∠B=∠C=35°，
∴∠DAB=180°-∠ADB-∠B=180°-90°-35°=55°．
故选B．
点评：本题考查的是圆周角定理，在解答此类题目时往往用到三角形的内角和是180°这一隐藏条件．
练习册系列答案
相关题目
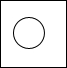如图，圆的直径是正方形边长的一半，圆位于正方形的内部．现随意地将飞镖掷向正方形内，则镖击中圆面部分的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
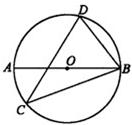10、如图，⊙O的直径是AB，CD是⊙O的弦，若∠D=70°，则∠ABC等于
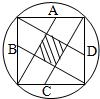11、如图，圆的直径是10厘米，A、B、C、D分别为正方形各边的中点，则图中阴影部分的面积是
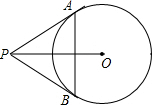如图，⊙O的直径是10cm，PA，PB切⊙O于点A、B两点，若PO=13cm，则△PAB的周长为
如图，⊙O的直径是10，弦AB=8，P为AB上的一动点，求OP的范围．