题目内容
 如图,在矩形ABCD中,AB=6,AD=8,P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为( )
如图,在矩形ABCD中,AB=6,AD=8,P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为( )| A、5 | B、4.8 | C、4.4 | D、4 |
考点:矩形的性质,三角形的面积
专题:
分析:过点A作AG⊥BD于G,连接PO,根据勾股定理列式求出BD的长度,再根据△ABD的面积求出AG,然后根据△AOD的面积求出PE+PF=AG,从而得解.
解答:解:如图,过点A作AG⊥BD于G,连接PO,
∵AB=6,AD=8,
∴BD=
=10,
∴S△ABD=
BD•AG=
AB•AD,
即
×10•AG=
×6×8,
解得AG=4.8,
在矩形ABCD中,AO=OD,
∴S△AOD=
AO•PE+
OD•PF=
OD•AG,
∴PE+PF=AG=4.8.
故选B.
∵AB=6,AD=8,

∴BD=
| AB2+AD2 |
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
解得AG=4.8,
在矩形ABCD中,AO=OD,
∴S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴PE+PF=AG=4.8.
故选B.
点评:本题考查了矩形的对角线相等且互相平分的性质,勾股定理的应用,根据三角形的面积求出PE+PF=AG是解题的关键,作辅助线是难点.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为( )
如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为( )A、
| ||||||
B、3-
| ||||||
C、
| ||||||
D、
|
下列整式计算中,结果正确的共有( )
-15x6÷
x2=-30x3;
(an-1)n+3=an2-3;
(-3x)4÷x•(-x)3=-81;
(-2a2b)3•(-
ab)2=-
a8b5.
-15x6÷
| 1 |
| 2 |
(an-1)n+3=an2-3;
(-3x)4÷x•(-x)3=-81;
(-2a2b)3•(-
| 2 |
| 3 |
| 32 |
| 9 |
| A、1个 | B、2个 | C、3个 | D、4个 |
在锐角三角形ABC中,∠A=29°,则下列哪个不可能是∠B的度数?( )
| A、47° | B、68° |
| C、75° | D、87° |
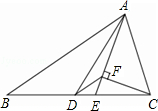 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为( )
如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为( )| A、3 | B、2.5 | C、1.5 | D、1 |
若2x=3,2y=5,则22x+y=( )
| A、11 | B、15 | C、30 | D、45 |