题目内容
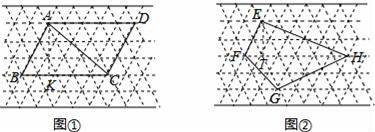
如图中的虚线网格我们称为正三角形网格,它的每一个小三角形都是边长为1个单位长度的正三角形,这样的三角形称为单位正三角形.
(1)图①中,已知四边形ABCD是平行四边形,求△ABC的面积和对角线AC的长;
(2)图②中,求四边形EFGH的面积.


【考点】平行四边形的性质;三角形的面积;等边三角形的性质;勾股定理.
【分析】(1)首先过点A作AK⊥BC于K,由每一个小三角形都是边长为1个单位长度的正三角形,可求得该小正三角形的高为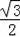
 ,则可求得△ABC的面积,然后由勾股定理求得对角线AC的长;
,则可求得△ABC的面积,然后由勾股定理求得对角线AC的长;
(2)首先过点E作ET⊥FH于T,即可得四边形EFGH的面积为:2S△EFH=2×
 ×ET×FH.
×ET×FH.
【解答】解:(1)由图①,过点A作AK⊥BC于K,
∵每一个小三角形都是边长为1个单位长度的正三角形.
∴该小正三角形的高为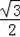
 ,
,
则:S△ABC=
 ×AK×CB=
×AK×CB=
 ×3×
×3×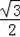
 ×CB=
×CB=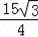
 ;
;
∵AK=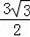
 ,BK=
,BK=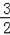
 ,
,
∴KC=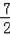
 ,
,
故由勾股定理可求得:AC=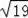
 .
.
(2)由图②,过点E作ET⊥FH于T,
又由题意可知:四边形EFGH的面积为:2S△EFH=2×
 ×ET×FH=ET×FH=2×
×ET×FH=ET×FH=2×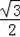
 ×6=6
×6=6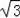
 .
.


练习册系列答案
相关题目
 是方程组
是方程组 的解,则
的解,则 、
、 的值为( )
的值为( ) B、
B、 C、
C、 D、
D、
 ﹣
﹣ +2
+2 ;
; 




 x+1=0,则
x+1=0,则
 等于( )
等于( )
 B.
B.
 C.
C.


 的解为
的解为 
 BC,试判断四边形BFCE是怎样的四边形,并证明你的结论.
BC,试判断四边形BFCE是怎样的四边形,并证明你的结论.
