题目内容
已知一个多边形的内角和与外角和之比为5:2,则它的边数是 .
考点:多边形内角与外角
专题:
分析:设内角的度数是5x°,则外角是2x°,根据内角与相邻的外角互补,即可求得外角的度数,然后根据外角和是360度,即可求得边数.
解答:解:设内角的度数是5x°,则外角是2x°,根据题意得:5x+2x=180,
解得:x=
,
则2x=
,
故多边形的边数是:
=7.
故答案为7.
解得:x=
| 180 |
| 7 |
则2x=
| 360 |
| 7 |
故多边形的边数是:
| 360 | ||
|
故答案为7.
点评:本题考查了多边形的计算,理解多边形的外角和是360度,外角和不随边数的变化而变化是关键.

练习册系列答案
相关题目
如果分式方程
-
=1有增根,那么增根可能是( )
| 2x |
| x+3 |
| k |
| x2-9 |
| A、-3 | B、3 | C、3或-3 | D、0 |
如果点P(x,y)在第三象限,那么(
)2-
的值为( )
| -x |
| y2 |
| A、x-y | B、-x-y |
| C、x+y | D、-x+y |
已知反比例函数y=
的图象经过点P(1,2),则这个函数的图象位于( )
| k |
| x |
| A、第二、三象限 |
| B、第一、三象限 |
| C、第二、四象限 |
| D、第三、四象限 |
 如图,已知AB=AC,AE=AD,BD=CE,说出∠1=∠2成立的理由.
如图,已知AB=AC,AE=AD,BD=CE,说出∠1=∠2成立的理由.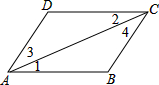 请你将证明过程补充完整(括号中填写理由)如图,AB∥CD,AD∥BC,那么AB=CD吗?AD=CB么?
请你将证明过程补充完整(括号中填写理由)如图,AB∥CD,AD∥BC,那么AB=CD吗?AD=CB么? 在直径为390mm的圆柱形油罐内装进一些油后,其横截面如图.若油的最大深度为120mm,求油面宽AB.
在直径为390mm的圆柱形油罐内装进一些油后,其横截面如图.若油的最大深度为120mm,求油面宽AB.