题目内容
15.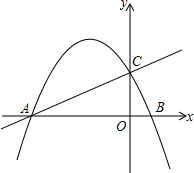 如图,已知直线y=$\frac{2}{5}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+4ax+b经过A、C两点,与x轴交于另-点B.
如图,已知直线y=$\frac{2}{5}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+4ax+b经过A、C两点,与x轴交于另-点B.(1)求抛物线的解析式:
(2)点Q在抛物线上,且S△AQC=S△BQC,求点Q的坐标.
分析 (1)先求出A、C两点坐标,再利用待定系数法即可解决问题.
(2)①分点Q在x轴上方时,根据平行线间的距离相等可得当CQ∥AB时,△AQC和△BQC面积相等,然后根据点Q与点C的纵坐标相等,利用抛物线解析式列式计算即可得解;②点Q在x轴下方时,设CQ与x轴相交于点D,根据△AQC和△BQC面积相等可知AD=BD,然后求出点D的坐标,再利用待定系数法求出直线CD的解析式,与抛物线联立求解即可得到点Q的坐标.
解答 解:(1)∵当y=0时,则有$\frac{2}{5}$x+2=0,解得x=-5,
∴点A的坐标为(-5,0),
∵当x=0时,则有y=2,
∴点C的坐标为(0,2),
∵抛物线y=ax2+4ax+b经过A、C两点,把(0,2)(-5,0)代入得
∴$\left\{\begin{array}{l}{b=2}\\{25a-20a+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{2}{5}}\\{b=2}\end{array}\right.$,
∴抛物线为y=-$\frac{2}{5}$x2-$\frac{8}{5}$x+2.
(2)①当Q在x轴上方时(如图1),
△ACQ和△BCQ同底,若它们的面积相等,则A、B到直线CQ的距离相等,即CQ∥AB;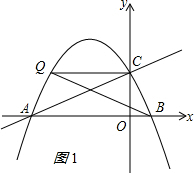
∵抛物线的对称轴为x=-2,
∴点Q坐标为(-4,2);
②当Q在x轴下方时(如图2),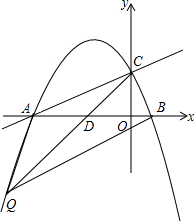
,设CQ与x轴交于点D,若△AQC和△BQC面积相等,则有AD=BD
令y=0,则-$\frac{2}{5}$x2-$\frac{8}{5}$x+2=0,解得x1=-5,x2=1,即AB=6
∴点D的坐标为(-2,0)
设直线CD的解析式为y=kx+b,把(0,2)(-2,0)代入得
$\left\{\begin{array}{l}{b=2}\\{-2k+b=0}\end{array}\right.$ 解得$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$
∴直线CD的解析式为y=x+2,
∵点Q在直线CD与抛物线上,
∴x+2=-$\frac{2}{5}$x2-$\frac{8}{5}$x+2,解得x1=0,x2=-$\frac{13}{2}$,
∴点Q坐标为(-$\frac{13}{2}$,-$\frac{9}{2}$);
∴点Q的坐标为(-4,2)或(-$\frac{13}{2}$,-$\frac{9}{2}$)
点评 本题考查了待定系数法求二次函数解析式及一次函数解析式,解题的关键是分类讨论点Q在抛物线上的不同位置,结合形成的三角形分析面积相等需具备的条件,数形结合思想在这里得到充分体现.

 阅读快车系列答案
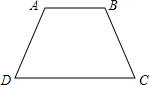
阅读快车系列答案 如图所示,由∠D=∠C,∠BAD=∠ABC推得△ABD≌△BAC,所用的判定定理的简称是( )
如图所示,由∠D=∠C,∠BAD=∠ABC推得△ABD≌△BAC,所用的判定定理的简称是( )| A. | ASA | B. | AAS | C. | SAS | D. | SSS |
| 一周内累计的读书时间(小时) | 6 | 8 | 10 | 11 |
| 人数(个) | 1 | 4 | 3 | 2 |
| A. | 众数是8 | B. | 中位数是9 | C. | 平均数是9 | D. | 方差是1.5 |
| A. | 2x2-3y-5=0 | B. | x2=2x | C. | $\frac{1}{x}$+4=x2 | D. | y2-$\sqrt{2y}$-3=0 |
 我们把:“有一组邻角相等的凸四边形”叫做“等邻角四边形”.
我们把:“有一组邻角相等的凸四边形”叫做“等邻角四边形”.