题目内容
如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E. AB、CO交于点M,连接OB.
(1)求证:∠ABO=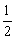 ∠ACB;
∠ACB;
(2)若sin∠EAB=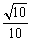 ,CB=12,求⊙O 的半径及
,CB=12,求⊙O 的半径及 的值.
的值.
 |
解:(1)证明:∵CA、CB为⊙O的切线,
∴ CA=CB, ∠BCO=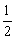 ∠ACB,∴∠CBO=90°.
∠ACB,∴∠CBO=90°.
∴ CO⊥AB.
∴ ∠ABO +∠CBM=∠BCO +∠CBM=90°.
∴ ∠ABO =∠BCO.
∴ ∠ABO=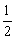 ∠ACB.
∠ACB.  (2) ∵ OA=OB, ∴∠EAB=∠ABO.
(2) ∵ OA=OB, ∴∠EAB=∠ABO.
∴ ∠BCO=∠EAB.
∵ sin∠BCO =sin∠EAB=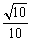 .
.
∴  =
= .
.
∵ CB=12,
∴ OB=4.即⊙O 的半径为4.
∴∠OBE=∠CAE=90°,∠E=∠E,
∴△OBE∽△CAE.
∴ =
= .
.
∵CA=CB=12,
∴ =
= .
.

练习册系列答案
相关题目
 的绝对值是
的绝对值是 B. 3 C.
B. 3 C. 
 与反比例函数
与反比例函数 的图象交于A(1,4),B(-2,
的图象交于A(1,4),B(-2, )两点,
)两点, 图象直接写出不等式
图象直接写出不等式 的解集.
的解集.

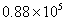 B.
B.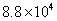 C.
C.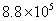 D.
D.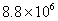
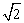 . 边A
. 边A B上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°. 设BE=x, MN=y,则能表示y与x的函数关系的大致图象是
B上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°. 设BE=x, MN=y,则能表示y与x的函数关系的大致图象是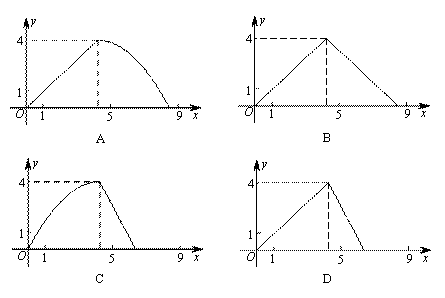
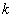 取任何实数,对于直线
取任何实数,对于直线 都会经过一个固定的点
都会经过一个固定的点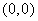 ,我们就称直线
,我们就称直线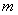 取任何实数,抛物线
取任何实数,抛物线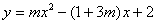 恒过定点
恒过定点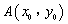 ,直接写出定点
,直接写出定点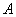 的坐标;
的坐标;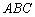 的一个顶点是(1)中的定点
的一个顶点是(1)中的定点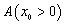 ,且
,且 ,
, 的角平分线分别是
的角平分线分别是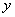 轴和直线
轴和直线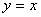 ,求边
,求边 所在直线的表达式;
所在直线的表达式;
 ,那么袋中的球共有 个.
,那么袋中的球共有 个.