题目内容
如图，已知△ABC是等边三角形，AB=4+2
，点D在AB上，点E在AC上，△ADE沿DE折叠后点A恰好落在BC上的A′点，且DA′⊥BC．则A′B的长是 ．
2 解：设A′B=x，
∵△ABC是等边三角形，
∴∠B=60°，
∵DA′⊥BC，
∴∠BDA′=90°﹣60°=30°，
∴BD=2A′B=2x，
由勾股定理得，A′D=
=
=x，
由翻折的性质得，AD=A′D=x，
所以，AB=BD+AD=2x+
x=4+2，
解得x=2，
即A′B=2．
练习册系列答案
相关题目
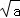=a；
B．
C．
D． 
