题目内容
15.已知方程x2+2x-1=0的两根分别是x1,x2,求$\frac{{x}_{2}}{{x}_{1}}+\frac{{x}_{1}}{{x}_{2}}$的值.分析 先根据根与系数的关系得出x1•x2与x1+x2的值,再代入代数式进行计算即可.
解答 解:∵方程x2+2x-1=0的两根分别是x1,x2,
∴x1•x2=-1,x1+x2=-2,
∴$\frac{{x}_{2}}{{x}_{1}}+\frac{{x}_{1}}{{x}_{2}}$=$\frac{({x}_{2}+{x}_{1})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{4+2}{-1}$=-6.
点评 本题考查的是根与系数的关系,熟记一元二次方程的根与系数的关系是解答此题的关键.

练习册系列答案
相关题目
3.体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
(1)全班有多少同学?
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几?
(4)画出适当的统计图表示上面的信息.
| 次数 | 60≤x<90 | 90≤x<120 | 120≤x<150 | 150≤x<180 | 180≤x<210 |
| 频数 | 16 | 25 | 9 | 7 | 3 |
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几?
(4)画出适当的统计图表示上面的信息.
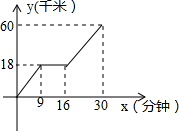 如图,是某汽车行驶的路程y(千米)与时间x(分钟)的函数关系图象,观察图中所提供的信息,解答下列问题.
如图,是某汽车行驶的路程y(千米)与时间x(分钟)的函数关系图象,观察图中所提供的信息,解答下列问题.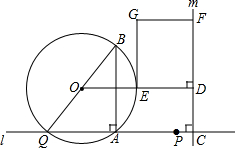 如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=$\frac{3}{2}$CD,以DE、DF为邻边作矩形DEGF.设AQ=3x
如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=$\frac{3}{2}$CD,以DE、DF为邻边作矩形DEGF.设AQ=3x