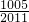题目内容
设直线l1:y=kx+k-1和直线l2:y=(k+1)x+k(k是正整数)及x轴围成的三角形面积是Sk,则S1+S2+S3+…+S2010=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:方程组
的解为
,直线y=kx+k-1与x轴的交点为(
,0),y=(k+1)x+k与x轴的交点为(
,0),先计算出SK的面积,再依据规律求解.
|
|
| 1-k |
| k |
| -k |
| k+1 |
解答:解:方程组
的解为
,
所以直线的交点是(-1,-1),
直线y=kx+k-1与x轴的交点为(
,0),y=(k+1)x+k与x轴的交点为(
,0),
∴Sk=
×|-1|×|
-
|=
|
-
|,
所以 S1+S2+S3+…+S2010=
(1-
+
-
+
-
+
-
)
=
×(1-
)
=
×
=
,
故选B.
|
|
所以直线的交点是(-1,-1),
直线y=kx+k-1与x轴的交点为(
| 1-k |
| k |
| -k |
| k+1 |
∴Sk=
| 1 |
| 2 |
| 1-k |
| k |
| -k |
| k+1 |
| 1 |
| 2 |
| 1 |
| k |
| 1 |
| k+1 |
所以 S1+S2+S3+…+S2010=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2010 |
| 1 |
| 2011 |
=
| 1 |
| 2 |
| 1 |
| 2011 |
=
| 1 |
| 2 |
| 2010 |
| 2011 |
=
| 1005 |
| 2011 |
故选B.
点评:本题考查了一次函数y=kx+b(k≠0,k,b为常数)的图象与两坐标轴的交点坐标特点,与x轴的交点的纵坐标为0,与y轴的交点的横坐标为0;也考查了坐标与线段的关系、三角形的面积公式以及分数的特殊运算方法.

练习册系列答案
相关题目
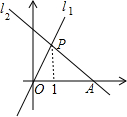 如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P.
如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P. (2013•历下区一模)如图,设直线l2:y=-2x+8与x轴相交于点N,与直线l1相交于点E(1,a),双曲线y=
(2013•历下区一模)如图,设直线l2:y=-2x+8与x轴相交于点N,与直线l1相交于点E(1,a),双曲线y=