题目内容
0是△ABC的内心，∠A=80°，则∠BOC的度数是（ ）A．160°
B．130°
C．100°
D．40°
【答案】分析：由三角形内切定义可知：OB、OC是∠ABC、∠ACB的角平分线，利用三角形内角和定理和角平分线定义可知关系式∠OBC+∠OCB=
（∠ABC+∠ACB），把对应数值代入即可求得∠BOC=130°．
解答：
解：∵OB、OC是∠ABC、∠ACB的角平分线，
∴∠OBC+∠OCB=
（∠ABC+∠ACB）=
（180°-80°）=50°，
∴∠BOC=180°-50°=130°；
故选B．
点评：本题通过三角形内切圆，考查切线的性质．
（∠ABC+∠ACB），把对应数值代入即可求得∠BOC=130°．解答：
解：∵OB、OC是∠ABC、∠ACB的角平分线，∴∠OBC+∠OCB=
（∠ABC+∠ACB）=（180°-80°）=50°，∴∠BOC=180°-50°=130°；
故选B．
点评：本题通过三角形内切圆，考查切线的性质．
练习册系列答案
阅读快车系列答案
相关题目
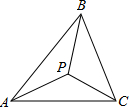如图，在△ABC中，点P是△ABC的内心，则∠PBC+∠PCA+∠PAB的度数为（ ）| A、150° | B、120° | C、90° | D、60° |
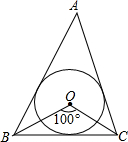如图所示，O是△ABC的内心，∠BOC=100°，则∠BAC=
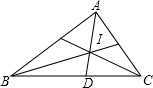如图，I是△ABC的内心，∠A=40°，则∠CIB=
如图，AB是圆O的直径，AB=10，点C是圆O上一动点（与A，B不重合），∠ACB的平分线交圆O于D．