题目内容
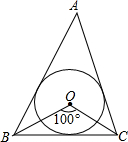 如图所示,O是△ABC的内心,∠BOC=100°,则∠BAC=
如图所示,O是△ABC的内心,∠BOC=100°,则∠BAC=分析:由三角形内切定义可知:OB、OC是∠ABC、∠ACB的角平分线.利用内角和定理先求得∠OBC+∠OCB=80°,所以可知∠OBC+∠OCB=
(∠ABC+∠ACB),把对应数值代入此关系式即可求得∠BAC的值.
| 1 |
| 2 |
解答:解:∵OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB=180°-100°=80°,而∠OBC+∠OCB=
(∠ABC+∠ACB)=80°,
∴∠ABC+∠ACB=160°,
∴∠BAC=180°-160°=20°.
∴∠OBC+∠OCB=180°-100°=80°,而∠OBC+∠OCB=
| 1 |
| 2 |
∴∠ABC+∠ACB=160°,
∴∠BAC=180°-160°=20°.
点评:本题通过三角形内切圆,考查切线的性质.

练习册系列答案
相关题目
 23、如图所示,CD是AB的垂直平分线,若AC=1.6cm,BD=2.3cm,则四边形ABCD的周长是( )
23、如图所示,CD是AB的垂直平分线,若AC=1.6cm,BD=2.3cm,则四边形ABCD的周长是( ) 12、如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C
12、如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C 4、已知:如图所示,E是AB延长线上的一点,AE=AC,AD平分∠BAC交BC于点D,BD=BE.求证:∠ABC=2∠C.
4、已知:如图所示,E是AB延长线上的一点,AE=AC,AD平分∠BAC交BC于点D,BD=BE.求证:∠ABC=2∠C. 如图所示,CD是AB的垂直平分线,若AC=10cm,BD=20cm,则四边形ACBD的周长为
如图所示,CD是AB的垂直平分线,若AC=10cm,BD=20cm,则四边形ACBD的周长为 如图所示,CD是AB的垂直平分线,若AC=2cm,BD=3cm,则四边形ACBD的周长是
如图所示,CD是AB的垂直平分线,若AC=2cm,BD=3cm,则四边形ACBD的周长是