题目内容
如图“L”形的图形的面积有如下四种表示方法:
①a2﹣b2;②a(a﹣b)+b(a﹣b);③(a+b)(a﹣b); ④(a﹣b)2.
其中正确的表示方法有( )

A.1种 B.2种 C.3种 D.4种
C【考点】平方差公式的几何背景.
【分析】利用不同的分割方法把:原图形剪成 两部分,它们分别是边长为a、a﹣b和b、a﹣b的矩形;沿对角线将原图分成两个直角梯形,将它们的对角线重合,拼成一个新的矩形;把原图形看作边长为a和边长为b的正方形的面积差.由此分别求得答案即可.
两部分,它们分别是边长为a、a﹣b和b、a﹣b的矩形;沿对角线将原图分成两个直角梯形,将它们的对角线重合,拼成一个新的矩形;把原图形看作边长为a和边长为b的正方形的面积差.由此分别求得答案即可.
【解答】解:如图①,
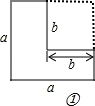
图①中,大正方形面积为a2,小正方形面积为b2,所以整个图形的面积为a2﹣b2;
如图②,
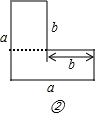
一个矩形的面积是b(a﹣b),另一个矩形的面积是a(a﹣b),所以整个图形的面积为a(a﹣b)+b(a﹣b);
如图③,
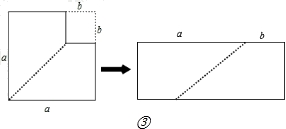
在图③中,拼成一长方形,长为a+b,宽为a﹣b,则面积为(a+b)(a﹣b).
综上所知:矩形的面积为①a2﹣b2;②a(a﹣b)+b(a﹣b);③(a+b)(a﹣b)共3种方法正确.
故选:C.
【点评】此题考查平方差公式的几何背景,掌握组合图形的拼接方法与面积的计算方法是解决问题的 关键.
关键.

 口算题天天练系列答案
口算题天天练系列答案某汽车行驶时油箱中余油量Q(千克)与行驶时间t(小时)的关系如下:
| 行驶时间t/h | 1 | 2 | 3 | 4 | 5 |
| 余油量Q/kg | 40﹣4 | 40﹣8 | 40﹣12 | 40﹣16 | 40﹣20 |
(1)写出用时间t表示余油量Q的代数式:Q=__________;
(2)当t= 时,余油量Q的值是__________;
时,余油量Q的值是__________;
(3)根据所列代数式回答,汽车行驶之前油箱中有油多少千克?
(4)邮箱中原有的汽油可供汽车行驶多少小时?
(直接写出每小问的结果)经检测,某棵小树在1~10年间的生长高度 符合一定的规律(如表):
符合一定的规律(如表):
| 年份 | 树高(cm) |
| 1 | 200 |
| 2 | 220 |
| 3 | 240 |
| 4 | 260 |
| 5 | 280 |
| … | … |
| 10 |
(1)第10年,这棵小树的高度为__________cm.
(2)树高h(cm)与年份n(1≤n≤10)之间的数量关系是h=__________(用含n的代数式表示h).
(3)如果把树高300cm称为标准树高,记为0cm,超过标准的高度记为正数,不足标准的高度记为负数,那么第2年的树高应记为__________cm.
 的倒数是__________.
的倒数是__________.
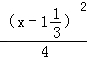 的值为正整数,你所取的x的值是__________.
的值为正整数,你所取的x的值是__________.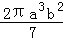 的系数是__________,次数是__________.
的系数是__________,次数是__________.