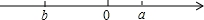题目内容
（直接写出每小问的结果）经检测，某棵小树在1～10年间的生长高度
符合一定的规律（如表）：
| 年份 | 树高（cm） |
| 1 | 200 |
| 2 | 220 |
| 3 | 240 |
| 4 | 260 |
| 5 | 280 |
| … | … |
| 10 |
（1）第10年，这棵小树的高度为__________cm．
（2）树高h（cm）与年份n（1≤n≤10）之间的数量关系是h=__________（用含n的代数式表示h）．
（3）如果把树高300cm称为标准树高，记为0cm，超过标准的高度记为正数，不足标准的高度记为负数，那么第2年的树高应记为__________cm．
【考点】列代数式；正数和负数；代数式求值．
【分析】（1）根据图表中的数据得到树高是每年以20cm的高度生长；
（2）根据数据写出函数解析式；
（3）由有理数的加减法进行解答．
【解答】解：（1）依题意得：200+（10﹣1）×20=380．
故答案是：380；
（2）依题意得：h=200+20（n﹣1）=180+20n．
故答案是：180+20n〔或200+20（n﹣1））；
（3）依题意得：300﹣220=80．
则那么第2年的树高应记为﹣80cm．
故答案是：﹣80．
【点评】本题考查了列代数式和代数式求值．解题的关键是弄懂题意，找到表格中数据间的等量关系．
练习册系列答案
相关题目
．
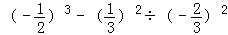