题目内容
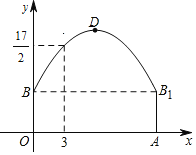
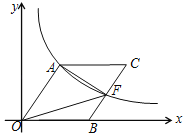
【题目】如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,点A的横纵坐标之比为3:4,反比例函数y=![]() (k>0)在第一象限内的图象经过点A,且与BC交于点F.
(k>0)在第一象限内的图象经过点A,且与BC交于点F.
(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标.
【答案】(1)y=![]() (x>0)(2)OA=
(x>0)(2)OA=![]() ,点C的坐标(
,点C的坐标(![]() ,
,![]() ).
).
【解析】
(1)过点A作AH⊥OB于H,根据已知条件得到sin∠AOB=![]() ,OA=10,求得AH=8,OH=6,于是得到结论;
,OA=10,求得AH=8,OH=6,于是得到结论;
(2)设OA=a(a>0),过点F作FM⊥x轴于M,过点C作CN⊥x轴于点N,根据平行四边形的性质得到OH=BN,根据已知条件得到AH=![]() a,OH=
a,OH=![]() a,于是得到S△AOH=
a,于是得到S△AOH=![]() ×
×![]() a
a![]() a=
a=![]() a2,求得S△OBF=6,得到S△BMF=
a2,求得S△OBF=6,得到S△BMF=![]() BMFM=
BMFM=![]() ×
×![]() a×
a×![]() a=
a=![]() a2,根据点A,F都在y=
a2,根据点A,F都在y=![]() 的图象上,得到S△AOH=S△FOM=
的图象上,得到S△AOH=S△FOM=![]() k,列方程即可得到结论.
k,列方程即可得到结论.
解:(1)过点A作AH⊥OB于H,
∵点A的横纵坐标之比为3:4,
∴sin∠AOB=![]() ,OA=10,
,OA=10,
∴AH=8,OH=6,
∴A点坐标为(6
8=![]() ,可得:k=48,
,可得:k=48,
∴反比例函数解析式:y=![]() (x>0);
(x>0);
(2)设OA=a(a>0),过点F作FM⊥x轴于M,过点C作CN⊥x轴于点N,
由平行四边形性质可证得OH=BN,
∵点A的横纵坐标之比为3:4,
∴sin∠AOB=![]() ,
,
∴AH=![]() a,OH=
a,OH=![]() a,
a,
∴S△AOH=![]() ×
×![]() a
a![]() a=
a=![]() a2,
a2,
∵S△AOF=12,
∴S平行四边形AOBC=24,
∵F为BC的中点,
∴S△OBF=6,
∵BF=![]() a,∠FBM=∠AOB,
a,∠FBM=∠AOB,
∴FM=![]() a,BM=
a,BM=![]() a,
a,
∴S△BMF=![]() BMFM=
BMFM=![]() ×
×![]() a×
a×![]() a=
a=![]() a2,
a2,
∴S△FOM=S△OBF+S△BMF=6+![]() a2,
a2,
∵点A,F都在y=![]() 的图象上,
的图象上,
∴S△AOH=S△FOM=![]() k,
k,
∴![]() a2=6+
a2=6+![]() a2,
a2,
∴a=![]() ,
,
∴OA=![]() ,
,
∴AH=![]() ,OH=2
,OH=2![]() ,
,
∵S平行四边形AOBC=OBAH=24,
∴OB=AC=3![]() ,
,
∴ON=OB+OH=5![]() ,
,
∴C(5![]() ,
,![]() ).
).


【题目】在函数学习中,我们经历了“确定函数表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时我们也学习了绝对值的意义![]() ,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
(1)求这个函数的表达式;
(2)用列表描点的方法画出该函数的图象;请你先把下面的表格补充完整,然后在下图所给的坐标系中画出该函数的图象;
x | … | ﹣6 | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
y | … |
| 0 | ﹣1 | ﹣2 | ﹣3 | ﹣2 |
| … |
(3)观察这个函数图象,并写出该函数的一条性质;
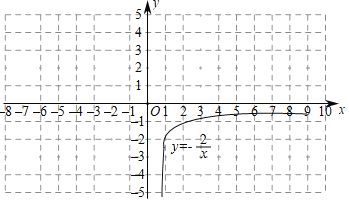
(4)已知函数y=![]() (x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2
(x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2![]() +4,
+4,![]() -2),(2
-2),(2![]() ﹣2
﹣2![]() ﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤
﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤![]() 的解集.
的解集.