题目内容
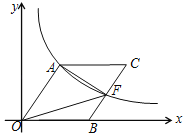
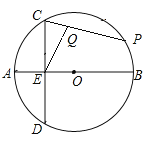
【题目】如图，
O的直径AB长为12，点E是半径OA的中点，过点E作CD⊥AB交O于点C、D，点P在
上运动，点Q在线段CP上，且PQ=2CQ，则EQ的最大值是_________.
【答案】
【解析】
延长CD到M点，使DM=DE，连接MP，可根据三角形相似求得EQ的长度等于
MP，当MP经过圆心时，此时MP有最大值，EQ为最大值，连接OD，根据勾股定理求出DE、OM，即可求得MP的长，则可求得EQ的最大值.
连接OD，延长CD到M点，使DM=DE，连接MO并延长交圆O与P点，此时MP有最大值.
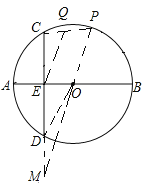
延长CD到M点，使DM=DE，连接MP，
∵CD⊥AB
∴CE=DE=DM
∵PQ=2CQ，EM=2CE
∴
又∠C=∠C
∴△QCE∽△PCM
∴
∴EQ=MP
当MP经过圆心时，此时MP有最大值，则EQ为最大值，
连接OD，
∵
O的直径AB长为12，点E是半径OA的中点，CD⊥AB
∴OD=6，OE=3，
∴DE=
∴EM=6
∴OM=
∴MP=OM+OP=
∴EQ=MP
故答案为：
练习册系列答案
阅读快车系列答案
相关题目
【题目】如图，在正方形
中，
，点
在正方形边上沿
运动（含端点），连接
，以为边，在线段右侧作正方形
，连接
、
.
小颖根据学习函数的经验，在点运动过程中，对线段、、的长度之间的关系进行了探究.
下面是小颖的探究过程，请补充完整：
（1）对于点在
、
边上的不同位置，画图、测量，得到了线段、、的长度的几组值，如下表：
位置 | 位置 | 位置 | 位置 | 位置 | 位置 | 位置 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
在、和的长度这三个量中，确定 的长度是自变量， 的长度和 的长度都是这个自变量的函数.
（2）在同一平面直角坐标系
中，画出（1）中所确定的函数的图象：
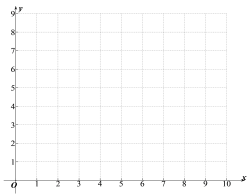
（3）结合函数图像，解决问题：
当
为等腰三角形时，的长约为
