题目内容
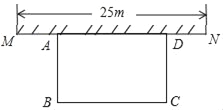
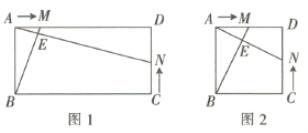
【题目】如图1,在矩形![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发向点
出发向点![]() 移动,速度为每秒1个单位长度,点
移动,速度为每秒1个单位长度,点![]() 从点
从点![]() 出发向点
出发向点![]() 移动,速度为每秒2个单位长度. 两点同时出发,且其中的任何一点到达终点后,另一点的移动同时停止.
移动,速度为每秒2个单位长度. 两点同时出发,且其中的任何一点到达终点后,另一点的移动同时停止.
(1)若两点的运动时间为![]() ,当
,当![]() 为何值时,
为何值时,![]() ?
?
(2)在(1)的情况下,猜想![]() 与
与![]() 的位置关系并证明你的结论.
的位置关系并证明你的结论.
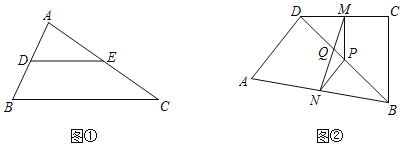
(3)①如图2,当![]() 时,其他条件不变,若(2)中的结论仍成立,则
时,其他条件不变,若(2)中的结论仍成立,则![]() _________.
_________.
②当![]() ,
,![]() 时,其他条件不变,若(2)中的结论仍成立,则
时,其他条件不变,若(2)中的结论仍成立,则![]() _________(用含
_________(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)①
,证明见解析;(3)①![]() ;②
;②![]()
【解析】
(1)根据相似三角形的性质,可得![]() ,进而列出方程,求出t的值.
,进而列出方程,求出t的值.
(2)根据相似三角形的性质,可得![]() ,进而根据等量关系以及矩形的性质,得出
,进而根据等量关系以及矩形的性质,得出![]() ,进而得出结论.
,进而得出结论.
(3)①根据全等三角形的判定,可得出△AMB≌△DNA,再根据全等三角形的性质,即可得出AM=DN,得出方程,求解即可得出答案.
解:(1)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
解得![]() .
.
(2)![]() .
.
证明:∵![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
(3)①∵![]()
∴∠ABE+∠BAE=90°
∵![]()
∴![]()
∵AD=AB,∠BAD=∠ADC=90°
∴△AMB≌△DNA
∴AM=DN
∴t=2-2t
∴t=![]()
②∵由①知![]() ,∠BAD=∠ADC=90°
,∠BAD=∠ADC=90°
∴![]()
∵![]()
∴![]() =n
=n
∴![]()
∴t=![]()

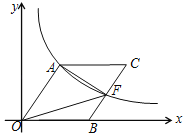
【题目】如图,在正方形![]() 中,
中,![]() ,点
,点![]() 在正方形边上沿
在正方形边上沿![]() 运动(含端点),连接
运动(含端点),连接![]() ,以
,以![]() 为边,在线段右侧作正方形
为边,在线段右侧作正方形![]() ,连接
,连接![]() 、
、![]() .
.
小颖根据学习函数的经验,在点![]() 运动过程中,对线段
运动过程中,对线段![]() 、
、![]() 、
、![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小颖的探究过程,请补充完整:
(1)对于点![]() 在
在![]() 、
、![]() 边上的不同位置,画图、测量,得到了线段
边上的不同位置,画图、测量,得到了线段![]() 、
、![]() 、
、![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 | 位置 | 位置 | 位置 | 位置 | 位置 | 位置 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
在![]() 、
、![]() 和
和![]() 的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数.
的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数.
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象:
中,画出(1)中所确定的函数的图象:
(3)结合函数图像,解决问题:
当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长约为
的长约为