题目内容
若等腰三角形的两边长分别为6和8,则周长为( )
| A、20或22 | B、20 |
| C、22 | D、无法确定 |
考点:等腰三角形的性质,三角形三边关系
专题:
分析:分6是腰长与底边两种情况分情况讨论,再利用三角形的三边关系判断是否能组成三角形.
解答:解:若6是腰长,则三角形的三边分别为6、6、8,
能组成三角形,
周长=6+6+8=20,
若6是底边长,则三角形的三边分别为6、8、8,
能组成三角形,
周长=6+8+8=22,
综上所述,三角形的周长为20或22.
故选A.
能组成三角形,
周长=6+6+8=20,
若6是底边长,则三角形的三边分别为6、8、8,
能组成三角形,
周长=6+8+8=22,
综上所述,三角形的周长为20或22.
故选A.
点评:本题考查了等腰三角形的性质,三角形的三边关系,难点在于分情况讨论.

练习册系列答案
相关题目
正六边形的中心角为( )
| A、60° | B、90° |
| C、120° | D、150° |
已知△ABC∽△A′B′C′,
=
,则△ABC与△A′B′C′的面积之比为( )
| AB |
| A′B′ |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
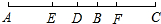 如图,已知线段AB和CD的公共部分BD=
如图,已知线段AB和CD的公共部分BD=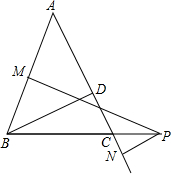 如图,在△ABC中,AB=AC,BD是AC边上的高,P为BC延长线上的一点,PM⊥AB,PN⊥AC,垂足分别是M,N,试问PM、PN与BD之间有何关系?
如图,在△ABC中,AB=AC,BD是AC边上的高,P为BC延长线上的一点,PM⊥AB,PN⊥AC,垂足分别是M,N,试问PM、PN与BD之间有何关系?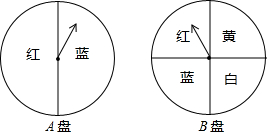 依次转动如图所示的两个转盘进行“配紫色”(红色与蓝色可配得紫色)游戏,每个转盘都被分成面积相等的几个扇形,请你用画树状图或列表的方法,求配得紫色的概率.
依次转动如图所示的两个转盘进行“配紫色”(红色与蓝色可配得紫色)游戏,每个转盘都被分成面积相等的几个扇形,请你用画树状图或列表的方法,求配得紫色的概率. 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为40,则OH的长等于
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为40,则OH的长等于 如图是一个正方体盒子的侧面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字是一对相反数.
如图是一个正方体盒子的侧面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字是一对相反数. 如图,已知:BE平分∠ABC,CF平分∠BCD,∠1=∠2,那么直线AB与CD的位置关系如何?
如图,已知:BE平分∠ABC,CF平分∠BCD,∠1=∠2,那么直线AB与CD的位置关系如何?