题目内容
 如图,梯形ABCD的对角线AC、BD交于点O,若S△AOD:S△ACD=1:4,则S△AOD:S△BOC的值为
如图,梯形ABCD的对角线AC、BD交于点O,若S△AOD:S△ACD=1:4,则S△AOD:S△BOC的值为
- A.1:3
- B.1:4
- C.1:9
- D.1:16
C
分析:先根据△AOD与△ACD面积的比,求出它们AD边上的高的比是1:4,△AOD的AD边上的高与△BOC的BC边上的高的比是1:(4-1)=1:3;又AD∥BC,所以△AOD∽△BOC,面积的比就等于相似比的平方.
解答:∵AD∥BC,
∴△AOD∽△BOC,
∵S△AOD:S△ACD=1:4,AD是两三角形的底边,
∴AD边上的高的比是1:4,
即△AOD与梯形的高的比是1:4,
∴△AOD与△BOC对应高的比为1:(4-1)=1:3,
∴S△AOD:S△BOC=1:9.
故选C.
点评:本题考查了相似三角形的判定和性质,对于本题可利用等底三角形面积的比等于高的比和相似三角形面积的比等于相似比的平方求解,难度适中.
分析:先根据△AOD与△ACD面积的比,求出它们AD边上的高的比是1:4,△AOD的AD边上的高与△BOC的BC边上的高的比是1:(4-1)=1:3;又AD∥BC,所以△AOD∽△BOC,面积的比就等于相似比的平方.
解答:∵AD∥BC,
∴△AOD∽△BOC,
∵S△AOD:S△ACD=1:4,AD是两三角形的底边,
∴AD边上的高的比是1:4,
即△AOD与梯形的高的比是1:4,
∴△AOD与△BOC对应高的比为1:(4-1)=1:3,
∴S△AOD:S△BOC=1:9.
故选C.
点评:本题考查了相似三角形的判定和性质,对于本题可利用等底三角形面积的比等于高的比和相似三角形面积的比等于相似比的平方求解,难度适中.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,梯形ABCD的对角线交于点O,有以下四个结论:
如图,梯形ABCD的对角线交于点O,有以下四个结论:①△AOB∽△COD,②△AOD∽△ACB,③S△DOC:S△AOD=DC:AB,④S△AOD=S△BOC,其中始终正确的有( )个.
| A、1 | B、2 | C、3 | D、4 |
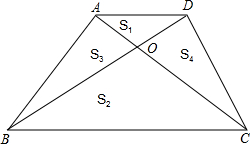 如图,梯形ABCD的对角线AC、BD相交于点O,△ADO的面积记作S1,△BCO的面积记作S2,△ABO的面积记作S3,△CDO的面积记作S4,则下列关系正确是( )
如图,梯形ABCD的对角线AC、BD相交于点O,△ADO的面积记作S1,△BCO的面积记作S2,△ABO的面积记作S3,△CDO的面积记作S4,则下列关系正确是( )| A、S1=S2 | B、S1×S2=S3×S4 | C、S1+S2=S4+S3 | D、S2=2S3 |
 14、如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有
14、如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有
 16、如图,梯形ABCD的对角线交于点O,有以下三个结论:
16、如图,梯形ABCD的对角线交于点O,有以下三个结论: 如图,梯形ABCD的面积为34cm2,AE=BF,CE与DF相交于O,△OCD的面积为11cm2,则阴影部分的面积为
如图,梯形ABCD的面积为34cm2,AE=BF,CE与DF相交于O,△OCD的面积为11cm2,则阴影部分的面积为