题目内容
4.已知a+b=$\frac{1}{2}$,a+c=2,那么代数式(b-c)2-3(c-b)+$\frac{9}{4}$的值是0.分析 根据等式的性质由a+b=$\frac{1}{2}$、a+c=2可得(a-c)的值,根据完全平方公式将原式分解因式可得(b-c+$\frac{3}{2}$)2,代入可得答案.
解答 解:∵a+b=$\frac{1}{2}$,a+c=2,
∴b-c=(a+b)-(a+c)=$\frac{1}{2}$-2=-$\frac{3}{2}$,
则(b-c)2-3(c-b)+$\frac{9}{4}$
=(b-c)2+2×$\frac{3}{2}$(b-c)+($\frac{3}{2}$)2
=(b-c+$\frac{3}{2}$)2
=(-$\frac{3}{2}$+$\frac{3}{2}$)2
=0,
故答案为:0.
点评 本题考查了因式分解、利用了等式的性质及完全平方公式,把(b-c)2-3(c-b)+$\frac{9}{4}$化成(b-c+$\frac{3}{2}$)2是解题关键.

练习册系列答案
相关题目
13. 如图是一个正方体的展开图,把展开图折叠成正方体后,“你”字一面相对的面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,“你”字一面相对的面上的字是( )
 如图是一个正方体的展开图,把展开图折叠成正方体后,“你”字一面相对的面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,“你”字一面相对的面上的字是( )| A. | 梦 | B. | 我 | C. | 中 | D. | 国 |
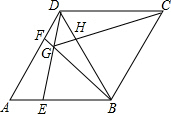 如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: