题目内容
10. 如图,点D是△ABC的边BC的延长线上一点,若∠A=60°,∠ACD=110°,则∠B=50°.
如图,点D是△ABC的边BC的延长线上一点,若∠A=60°,∠ACD=110°,则∠B=50°.
分析 根据三角形的一个外角等于和它不相邻的两个内角的和计算即可.
解答 解:∵∠ACD是△ABC的一个外角,
∴∠ACD=∠A+∠B,
∴∠B=∠ACD-∠A=50°,
故答案为:50°.
点评 本题考查的是三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
15.在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,且∠A:∠B:∠C=1:1:2,则下列说法中,错误的是( )
| A. | ∠C=90° | B. | a=b | C. | c2=2a2 | D. | a2=b2-c2 |
2.下列式子是分式的是( )
| A. | $\frac{a}{4}$ | B. | $\frac{1}{2}{x}^{2}$ | C. | $\frac{x}{π}$ | D. | $\frac{1}{a}$ |
19.已知$\frac{a}{b}=\frac{c}{d}=\frac{2}{3}$(b+d≠0),则$\frac{a+c}{b+d}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |

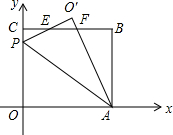 在平面直角坐标系中,O是坐标原点,矩OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8),点P是y轴上的一个动点,将△OAP沿AP翻折得到:△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.
在平面直角坐标系中,O是坐标原点,矩OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8),点P是y轴上的一个动点,将△OAP沿AP翻折得到:△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.