题目内容
2.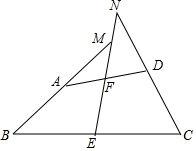 如图,在四边形ABCD中,AB=CD,点E、F分别是BC、AD的中点,连结EF并延长分别与BA、CD的延长线交于点M、N,∠BME与∠CNE的大小关系如何?试说明理由.
如图,在四边形ABCD中,AB=CD,点E、F分别是BC、AD的中点,连结EF并延长分别与BA、CD的延长线交于点M、N,∠BME与∠CNE的大小关系如何?试说明理由.
分析 如图,连结BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.
解答 解:∠BME=∠CNE,理由如下:
连结BD,取BD的中点H,连接HE、HF,
∵点E、F分别是BC、AD的中点,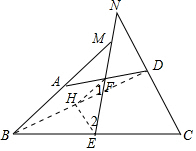
∴HF∥BM.HF=$\frac{1}{2}$AB,HE∥CD,HE=$\frac{1}{2}$CD,
∴∠1=∠BME,∠2=∠ENC,
∵AB=CD,
∴HF=HE,
∴∠1=∠2,
∴∠BME=∠CNE.
点评 此题考查了三角形的中位线定理,解答此题的关键是作出三条辅助线,构造出和中位线定理相关的图形.此题结构精巧,考查范围广,综合性强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 按要求在已知图形上作图.
按要求在已知图形上作图.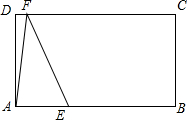 在矩形ABCD中,AB=6,AD=2$\sqrt{3}$,E是AB边上一点,AE=2,F是直线CD上一动点,将△AEF沿直线EF折叠,点A的对应点为点A′,当点E、A′、C三点在一条直线上时,DF的长度为6+2$\sqrt{7}$或6-2$\sqrt{7}$.
在矩形ABCD中,AB=6,AD=2$\sqrt{3}$,E是AB边上一点,AE=2,F是直线CD上一动点,将△AEF沿直线EF折叠,点A的对应点为点A′,当点E、A′、C三点在一条直线上时,DF的长度为6+2$\sqrt{7}$或6-2$\sqrt{7}$.
 如图,△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,且CD=BD.
如图,△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,且CD=BD.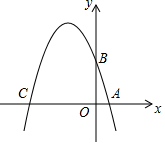 如图,在平面直角坐标系xOy中,A、B、C三点分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.
如图,在平面直角坐标系xOy中,A、B、C三点分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.