题目内容
如图,两个反比例函数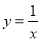 和
和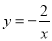 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为( )
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为( )
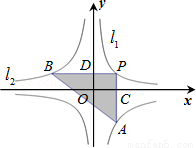
A. 3 B. 4 C. 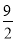 D. 5
D. 5
如图是二次函数y=ax2+bx+c的图象,下列结论: ①二次三项式ax2+bx+c的最大值为4;
②4a+2b+c<0;
③一元二次方程ax2+bx+c=1的两根之和为﹣1;
④使y≤3成立的x的取值范围是x≥0.
其中正确的个数有( )
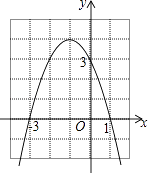
A. 1个 B. 2个 C. 3个 D. 4个
查看答案某同学在用描点法画二次函数y=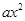 +bx+c的图象时,列出了下面的表格:
+bx+c的图象时,列出了下面的表格:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣11 | ﹣2 | 1 | ﹣2 | ﹣5 | … |
由于粗心,他算错了其中一个y值,则这个错误的数值是( ).
A.﹣11 B.﹣2 C.1 D.﹣5
查看答案若圆锥的底面积为16πcm2,母线长为12cm,则它的侧面展开图的圆心角为( )
A. 240° B. 120° C. 180° D. 90°
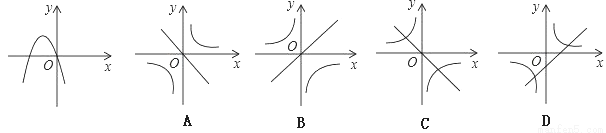
查看答案已知二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=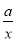 在同一平面直角坐标系中的图象大致是( )
在同一平面直角坐标系中的图象大致是( )
如图,正方形ABCD内接于⊙O,⊙O的直径为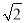 分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( ).
分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( ).
A.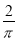 B.
B.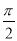 C.
C.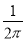 D.
D.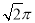
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案下列命题中,不正确的是( )
A. 垂直平分弦的直线经过圆心 B. 平分弦的直径一定垂直于弦
C. 平行弦所夹的两条弧相等  D. 垂直于弦的直径必平分弦所对的弧
D. 垂直于弦的直径必平分弦所对的弧
二次函数y=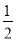 (x﹣1)2+2的图象可由y=
(x﹣1)2+2的图象可由y=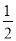 x2的图象( )
x2的图象( )
A. 向左平移1个单位,再向下平移2个单位得到
B. 向左平移1个单位,再向上平移2个单位得到
C. 向右平移1个单位,再向下平移2个单位得到
D. 向右平移1个单位,再向上平移2个单位得到
查看答案如图,将正方形图案绕中心O旋转180°后,得到的图案是( )
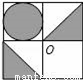
A.  B.
B.  C.
C. 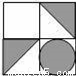 D.
D. 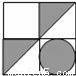
下列方程是关于x的一元二次方程的是( )
A. ax2+bx+c=0 B. 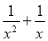 =2 C. x2+2x=x2﹣1 D. 3(x+1)2=2(x+1)
=2 C. x2+2x=x2﹣1 D. 3(x+1)2=2(x+1)
阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
【解析】
∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)已知x2﹣2xy+2y2+6y+9=0,求xy的值;
(2)已知△ABC的三边长a、b、c都是正整数,且满足a2+b2﹣10a﹣12b+61=0,求△ABC的最大边c的值;
(3)已知a﹣b=8,ab+c2﹣16c+80=0,求a+b+c的值.
查看答案某商家预测一种衬衫能畅销市场,就用12000元购进了一批这种衬衫,上市后果然供不应求,商家又用了26400元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但每件进价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫都按每件150元的价格销售,则两批衬衫全部售完后的利润是多少元?
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在三角形ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE=__________.

函数 是
是 关于
关于 的反比例函数,则
的反比例函数,则 _______.
_______.
如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离OH=_____.
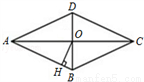
一个直角三角形斜边上的高与中线分别是5㎝和6㎝,则它的面积是______ 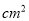 .
.
反比例函数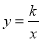 经过点(-2,1),则一次函数
经过点(-2,1),则一次函数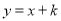 的图象经过点(-1,_____).
的图象经过点(-1,_____).
方程(x+2)2=x+2的解是 ____________________.
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
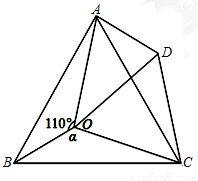
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.
一次函数y=kx+b的图象与反比例函数y=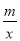 的图象交于点A(2,1),B(-1,n)两点.
的图象交于点A(2,1),B(-1,n)两点.
(1)求反比例函数的解析式;
(2)求一次例函数的解析式;
(3)求△AOB的面积.
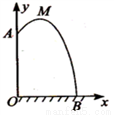
如图所示, 有一建筑工地从10m 高的窗A处用水管向外喷水,喷出的水呈抛物线状,如果抛物线的最高点M 离墙1m,离地面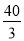 m.
m.
(1)求抛物线的解析式;
(2)求水流落地点B离墙的距离OB.
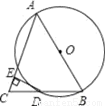
如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.
商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案已知抛物线经过三点A(2,6)、B(-1,0)、C(3,0).
求这条抛物线所对应的二次函数的解析式;
(2)写出它的对称轴和顶点坐标.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
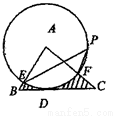
如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是__________(结果保留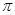 )
)
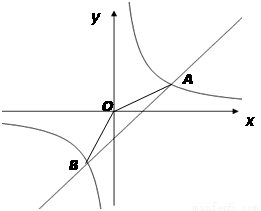
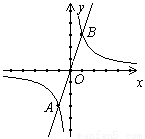
如图,反比例函数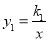 和正比例函数y2=k2x 的图象交于A(-1,-3)、B(1,3)两点,若
和正比例函数y2=k2x 的图象交于A(-1,-3)、B(1,3)两点,若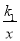 >k2x,则x的取值范围是___________________.
>k2x,则x的取值范围是___________________.
已知点A(-1,y1)、B(2,y2)都在双曲线y= 上,且y1>y2,则m的取值范围是______________
上,且y1>y2,则m的取值范围是______________
若抛物线y=x2-2x-3与x轴分别交于A,B两点,则AB的长为 ______.
查看答案直线y=x+3上有一点P(3,a),则点P关于原点的对称点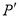 为___________.
为___________.
如图,两个反比例函数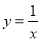 和
和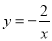 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为( )
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为( )

A. 3 B. 4 C. 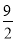 D. 5
D. 5
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
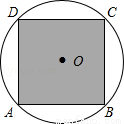
如图,正方形ABCD内接于⊙O,⊙O的直径为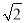 分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( ).
分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( ).

A.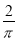 B.
B.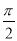 C.
C.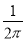 D.
D.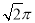
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么线段OE的长为( )
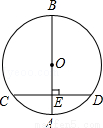
A.6 B.5 C.4 D.3
查看答案反比例函数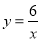 图象上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是( )
图象上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A. y2<y1<y3 B. y1<y2<y3 C. y3<y1<y2 D. y3<y2<y1
查看答案一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( )
A. 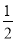 B.
B. 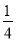 C.
C. 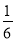 D.
D. 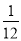
如图,⊙O是△ABC的外接圆,∠OCB=40°则∠A的度数等于( )
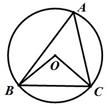
A. 60° B. 50° C. 40° D. 30°
查看答案在下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.  B .
B . C .
C . D.
D. 
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
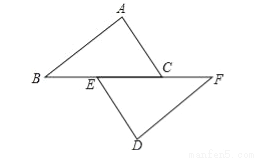
如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.
直线y=kx+4经过点(1,2),求不等式kx+4≥0的解集.
查看答案某校开展“节约每一滴水”活动,为了了解开展活动的一个月以来节约用水的病况,从八年级的400名同学中选出20名同学统计了解各自家庭一个月的节水情况,见下表:
节水(m3) | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 |
家庭数(个) | 2 | 4 | 6 | 7 | 1 |
分别求出这20个家庭节水的中位数和众数.请你估计这400名同学的家庭一个月节约用水的总量大约是多少m3?
查看答案如图,△ABC和△ABD中,∠C=∠D=Rt∠,E是BC边上的中线.请你说明CE=DE的理由.
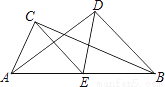
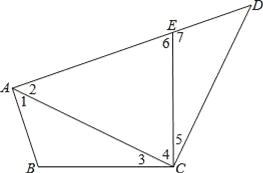
如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.
如果关于x的不等式k﹣x+6>0的正整数解为1、2、3,那么k的取值范围是多少?
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在△ABC中,∠B=∠C,AD为△ABC的中线,那么下列结论错误的是( )
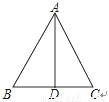
A. △ABD≌△ACD B. AD为△ABC的高线 C. AD为△ABC的角平分线 D. △ABC是等边三角形
D 【解析】试题解析:∵∠B=∠C, ∴AB=AC, ∵AD是△ABC的中线, ∴AD⊥BC,∠BAD=∠CAD,即AD是△ABC的高,AD为△ABC的角平分线, ∴∠ADB=∠ADC=90°, 在△ABD和△ACD中 ∴△ABD≌△ACD, 即选项A、B、C都正确, 根据已知只能推出AC=AB,不能推出AC、AB和BC的关系, 即不能得...下列命题中是真命题的是( )
A. 确定性事件发生的概率为1;
B. 平分弦的直径垂直于弦;
C. 正n边形都是轴对称图形,并且有n条对称轴;
D. 两边及其一边的对角对应相等的两个三角形全等。
查看答案用a、b、c作三角形的三边,其中不能构成直角三角形的是( )
A. a2=(b+c)(b﹣c) B. a:b:c=1: 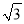 :2
:2
C. a=32,b=42,c=52 D. a=5,b=12,c=13
查看答案如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
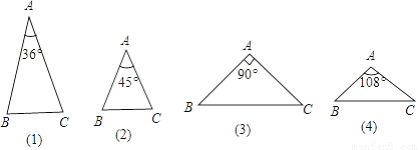
A. (1)(2)(3) B. (1)(3)(4) C. (2)(3)(4) D. (1)(2)(4)
查看答案如图,PB⊥AB于B,PC⊥AC于C,且PB=PC,则△APB≌△APC的理由是( )
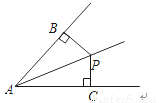
A. SAS B. ASA C. HL D. AAS
查看答案如图,在△ABC中,AB=AC=5,P是BC边上除B,C点外的任意一点,则代数式AP2+PB·PC等于 ( )
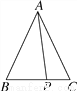
A. 25 B. 15 C. 20 D. 30
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

