题目内容
12.若式子$\sqrt{k-1}$+(k-1)0有意义,则一次函数y=(k-1)x+1-k的图象可能是( )| A. |  | B. |  | C. |  | D. |  |
分析 首先根据二次根式中的被开方数是非负数,以及a0=1(a≠0),判断出k的取值范围,然后判断出k-1、1-k的正负,再根据一次函数的图象与系数的关系,判断出一次函数y=(k-1)x+1-k的图象可能是哪个即可.
解答 解:∵式子$\sqrt{k-1}$+(k-1)0有意义,
∴$\left\{\begin{array}{l}{k-1≥0}\\{k-1≠0}\end{array}\right.$
解得k>1,
∴k-1>0,1-k<0,
∴一次函数y=(k-1)x+1-k的图象可能是: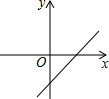 .
.
故选:A.
点评 (1)此题主要考查了一次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.
(2)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.
(3)此题还考查了二次根式有意义的条件,要熟练掌握,解答此题的关键是要明确:二次根式中的被开方数是非负数.

练习册系列答案
相关题目
7.2015年5月17日是第25个全国助残日,今年全国助残日的主题是“关注孤独症儿童,走向美好未来”.第二次全国残疾人抽样调查结果显示,我国0~6岁精神残疾儿童约为11.1万人.11.1万用科学记数法表示为( )
| A. | 1.11×104 | B. | 11.1×104 | C. | 1.11×105 | D. | 1.11×106 |
4.某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
| 劳动时间(小时) | 3 | 3.5 | 4 | 4.5 |
| 人 数 | 1 | 1 | 2 | 1 |
| A. | 中位数是4,平均数是3.75 | B. | 众数是4,平均数是3.75 | ||
| C. | 中位数是4,平均数是3.8 | D. | 众数是2,平均数是3.8 |
1.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (-a+b)(a+b)=b2-a2 | C. | (a3)4=a7 | D. | a3+a5=a8 |
 如图,⊙O的半径为5,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.
如图,⊙O的半径为5,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.


