题目内容
在Rt△ABC中,已知∠C=90°,sinA=
且AB=15,则AC= ,BC= .
| 3 |
| 5 |
考点:解直角三角形
专题:
分析:根据角A的正弦求出AB,根据勾股定理求出AC即可.
解答:
解:∵sinA=
=
,AB=15,
∴BC=9,
由勾股定理得:AC=
=
=12,
故答案为:12,9.

解:∵sinA=
| BC |
| AB |
| 3 |
| 5 |
∴BC=9,
由勾股定理得:AC=
| AB2-BC2 |
| 152-92 |
故答案为:12,9.
点评:本题考查了锐角三角函数的定义和勾股定理的应用,注意:在Rt△ACB中,∠ACB=90°,则sinA=
,cosA=
,tanA=
.
| ∠A的对边 |
| 斜边 |
| ∠A的邻边 |
| 斜边 |
| ∠A的对边 |
| ∠A的邻边 |

练习册系列答案
相关题目
下列旋转图形中,10°,20°,30°,40°,…,90°,180°都是旋转角度的是( )
| A、正方形 | B、正十边形 |
| C、正二十边形 | D、正三十六边形 |
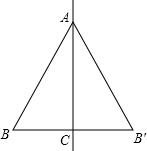 在Rt△ABC中,斜边AB=2BC,以直线AC为对称轴,点B的对称点是B′,如图,则与线段BC相等的线段是
在Rt△ABC中,斜边AB=2BC,以直线AC为对称轴,点B的对称点是B′,如图,则与线段BC相等的线段是 如图,以点A为顶点的三角形有
如图,以点A为顶点的三角形有