题目内容
如果关于x的方程x2-px-q=0（p，q是正整数）的正根小于3，那么这样的方程个数是（ ）
| A、5 | B、6 | C、7 | D、8 |
考点：一元二次方程根的分布
专题：
分析：题中条件：“二次方程x2-px-q=0（p，q是正整数）的正根小于3”转化为函数的零点问题，利用函数的图象解决问题．
解答：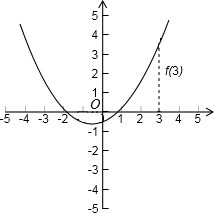
解：设f（x）=x2-px-q（p，q是正整数），
画出函数f（x） 的图象：
观察图得：
∵f（0）=-q＜0，f（3）=9-3p-q＞0，
∴3p+q＜9，又p，q∈N*，
∴当p=1时，q=1，2，3，4，5．当p=2时，q=1，2．
故这样的方程个数是7个．
故选：C．
解：设f（x）=x2-px-q（p，q是正整数），画出函数f（x） 的图象：
观察图得：
∵f（0）=-q＜0，f（3）=9-3p-q＞0，
∴3p+q＜9，又p，q∈N*，
∴当p=1时，q=1，2，3，4，5．当p=2时，q=1，2．
故这样的方程个数是7个．
故选：C．
点评：本题考查函数的零点与方程根的关系以及数形结合的思想，华罗庚曾说过：“数缺形时少直观，形缺数时难入微．数形结合百般好，隔离分家万事非．”数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质．
练习册系列答案
阅读快车系列答案
相关题目
已知a、b为实数且ab=1，设P=
+
，Q=
+
；则P、Q的大小关系为（ ）
| 1 |
| a+1 |
| 1 |
| b+1 |
| a |
| a+1 |
| b |
| b+1 |
| A、P＞Q | B、P＜Q |
| C、P=Q | D、大小关系不能确定 |
下列各式计算正确的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
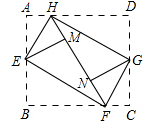如图，将矩形ABCD的四个角向内折起，恰好拼成一个既无缝隙又无重叠的四边形EFGH，若EH=3，EF=4，那么线段AH：HD=