题目内容
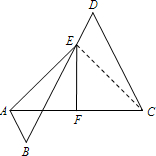
 如图,AB∥CD,点E在线段BD上,BE=CD,ED=AB,F是线段AC的中点,连接AE、EF.试判断EF与AC的位置关系,并说明理由.
如图,AB∥CD,点E在线段BD上,BE=CD,ED=AB,F是线段AC的中点,连接AE、EF.试判断EF与AC的位置关系,并说明理由.分析:连接EC,由条件可以证明△BAE≌△DEC,就可以得出AE=CE,再由条件就可以得出△AEF≌△CEF就可以得出∠AFE=∠CFE,就可以得出结论.
解答:解:EF⊥AC.
理由:连接EC
∵AB∥CD,
∴∠B=∠D.
在△BAE和△DEC中
,
∴△BAE≌△DEC(SAS),
∴AE=CE.
∵F是线段AC的中点,
∴AF=CF.
在△AEF≌△CEF
,
∴△AEF≌△CEF(SSS)
∴∠AFE=∠CFE.
∵∠AFE+∠CFE=180°,
∴∠AFE=90°,
∴EF⊥AC.
理由:连接EC
∵AB∥CD,
∴∠B=∠D.
在△BAE和△DEC中
|

∴△BAE≌△DEC(SAS),
∴AE=CE.
∵F是线段AC的中点,
∴AF=CF.
在△AEF≌△CEF
|
∴△AEF≌△CEF(SSS)
∴∠AFE=∠CFE.
∵∠AFE+∠CFE=180°,
∴∠AFE=90°,
∴EF⊥AC.
点评:本题考查了垂直的判定的运用,平行线的性质的运用,全等三角形的判定及性质的运用,解答时添加辅助线是难点,证明三角形全等是关键.

练习册系列答案
相关题目
 8、如图,AB∥CD,点E在CB的延长线上,若∠ABE=60°,则∠ECD的度数为( )
8、如图,AB∥CD,点E在CB的延长线上,若∠ABE=60°,则∠ECD的度数为( ) (2013•通州区一模)如图,AB∥CD,点E在AB上,且DC=DE,∠AEC=70°,则∠D的度数是
(2013•通州区一模)如图,AB∥CD,点E在AB上,且DC=DE,∠AEC=70°,则∠D的度数是 (2013•顺义区一模)如图,AB∥CD,点E在BC上,∠BED=68°,∠D=38°,则∠B的度数为( )
(2013•顺义区一模)如图,AB∥CD,点E在BC上,∠BED=68°,∠D=38°,则∠B的度数为( ) (2013•重庆模拟)如图,AB∥CD,点E在CD上,EG与AB交于F,DF⊥EG于F,若∠D=25°,则∠GFB的度数是( )
(2013•重庆模拟)如图,AB∥CD,点E在CD上,EG与AB交于F,DF⊥EG于F,若∠D=25°,则∠GFB的度数是( ) 如图,AB⊥CD于点O,EF为过点O的一条直线,若∠1=55°,则∠2=
如图,AB⊥CD于点O,EF为过点O的一条直线,若∠1=55°,则∠2=