题目内容
18.关于x的方程a(x+m)2+n=0(a,m,n均为常数,m≠0)的解是x1=-2,x2=3,则方程a(x+m-5)2+n=0的解是( )| A. | x1=-2,x2=3 | B. | x1=-7,x2=-2 | C. | x1=3,x2=-2 | D. | x1=3,x2=8 |
分析 把后面一个方程中的x-5看作整体,相当于前面一个方程中的x求解.
解答 解:∵关于x的方程a(x+m)2+n=0的解是x1=-2,x2=3,(m,n,p均为常数,m≠0),
∴方程a(x+m-5)2+n=0变形为a[(x-5)+m]2+n=0,即此方程中x-5=-2或x-5=3,
解得x=3或x=8.
故选D.
点评 此题主要考查了方程解的定义.注意由两个方程的特点进行简便计算.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
8.在-3,-$\frac{1}{2}$,0,2四个数中,是负整数的是( )
| A. | -3 | B. | -$\frac{1}{2}$ | C. | 0 | D. | 2 |
9.化简:(-m)12÷(-m)3等于( )
| A. | m4 | B. | -m4 | C. | m9 | D. | -m9 |
10.在Rt△ABC中,∠C=90°,若斜边上的高为h,sinA=$\frac{3}{5}$,则AB的长等于( )
| A. | $\frac{5}{4}$h | B. | $\frac{5}{3}$h | C. | $\frac{25}{12}$h | D. | $\frac{12}{25}$h |
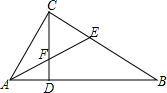 如图,△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC交CD于F,交BC于E,试说明△CEF是等腰三角形.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC交CD于F,交BC于E,试说明△CEF是等腰三角形.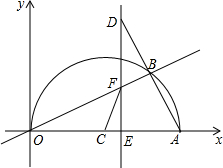 平面直角坐标系中,已知点A的坐标为(10,0),已知点C为中点,以c为圆心作圆,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.
平面直角坐标系中,已知点A的坐标为(10,0),已知点C为中点,以c为圆心作圆,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.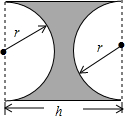 一零件的横截面(阴影部分)如图所示,你能用关于r,h的多项式表示此零件的横截面积吗?这个多项式能分解因素吗?若r=4cm,h=10cm,求这个零件的横截面积.(结果精确到个位).
一零件的横截面(阴影部分)如图所示,你能用关于r,h的多项式表示此零件的横截面积吗?这个多项式能分解因素吗?若r=4cm,h=10cm,求这个零件的横截面积.(结果精确到个位).