题目内容
11.抛物线y=a(x-h)2+k与x轴交于A(-1,0),B(7,0)两点,给出以下判断:①若k=2,则抛物线的解析式为y=-$\frac{1}{8}$(x-3)2+2
②当x>3时,y随x的增大而减小
③点P为抛物线上任意一点,使△ABP为等腰三角形的点P至少有3个
④点P为抛物线上任意一点,若使△ABP的面积为12的点P至少有三个,则抛物线的顶点纵坐标k必须满足k≥3.
其中正确的是①③(填序号).
分析 ①先根据抛物线的对称性,求得h=3,然后将k=2,和点A或点B的坐标代入可求得抛物线的解析式;
②可分为a>0和a<0两种情况;
③根据等腰三角形的性质和抛物线的对称性可判断;
④根据a>0和a<0两种情况讨论即可.
解答 解:①由抛物线的对称性可知:h=3,将k=2,A(-1,0)代入得:a×(4)2+2=0,
解得:a=$\frac{1}{8}$.
∴抛物线的解析式为y=-$\frac{1}{8}$(x-3)2+2,故①正确;
②当a>0,x>3时,y随x的增大而增大;当a<0,x>3时,y随x的增大而减小,故②错误;
③当AP=PB时,点P为抛物线的顶点,当AP=AB时,点P在抛物线上;当BP=BA时,点P也在抛物线,故③正确;
④当a>0,k≤-3时,使△ABP的面积为12的点P至少有三个;当a<0,k≥3时,使△ABP的面积为12的点P至少有三个,故④错误.
故答案为:①③.
点评 本题主要考查的是抛物线与x轴的交点问题,分类讨论是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
16.一个数的相反数比本身大,那么这个数必定是( )
| A. | 正数 | B. | 负数 | C. | 整数 | D. | 0 |
20.如果把分式$\frac{x+y}{2y}$中的x、y的值都扩大2倍,那么分式的值( )
| A. | 扩大2倍 | B. | 扩大6倍 | C. | 扩大3倍 | D. | 不变 |
1.设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的圆的圆心O在直线l上运动,A、O两点之间的距离为d.
(1)如图①,当r<a时,填表:
(2)如图②,⊙O与正方形有5个公共点B、C、D、E、F,求此时r与a之间的数量关系.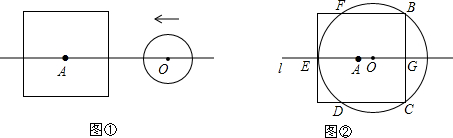
(3)由(1)可知,d、a、r之间的数量关系和⊙O的与正方形的公共点个数密切相关,当r=a时,请根据d、a、r之间的数量关系,判断⊙O与正方形的公共点个数.
(4)当r与a之间满足(2)中的数量关系,⊙O与正方形的公共点个数为0,1,2,5或8.
(1)如图①,当r<a时,填表:
| d,a,r之间的关系 | ⊙O与正方形的公共点个数 |
| d>a+r | 0 |
| d=a+r | 1 |
| a-r<d<a+r | 2 |
| d=a-r | 1 |
| 0≤d<a-r | 0 |
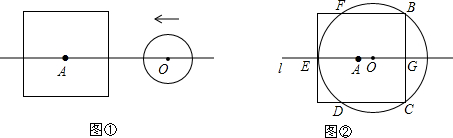
(3)由(1)可知,d、a、r之间的数量关系和⊙O的与正方形的公共点个数密切相关,当r=a时,请根据d、a、r之间的数量关系,判断⊙O与正方形的公共点个数.
(4)当r与a之间满足(2)中的数量关系,⊙O与正方形的公共点个数为0,1,2,5或8.