题目内容
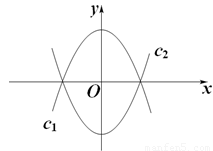
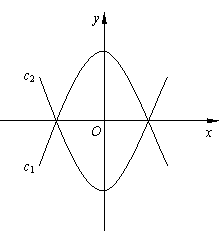
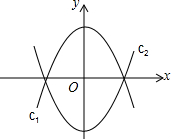
将抛物线c1:y= 沿x轴翻折,得抛物线c2,如图所示。
沿x轴翻折,得抛物线c2,如图所示。
(1)请直接写出抛物线c2的表达式;
(2)现将抛物线c1向左平移m个单位长度,平移后得到的新抛物线的顶点为M,与x轴的交点从左到右依次为A,B;将抛物线c2向右也平移m个单位长度,平移后得到的新抛物线的顶点为N,与x轴交点从左到右依次为D,E。
①当B,D是线段AE的三等分点时,求m的值;
②在平移过程中,是否存在以点A,N,E,M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由。
 沿x轴翻折,得抛物线c2,如图所示。
沿x轴翻折,得抛物线c2,如图所示。(1)请直接写出抛物线c2的表达式;
(2)现将抛物线c1向左平移m个单位长度,平移后得到的新抛物线的顶点为M,与x轴的交点从左到右依次为A,B;将抛物线c2向右也平移m个单位长度,平移后得到的新抛物线的顶点为N,与x轴交点从左到右依次为D,E。
①当B,D是线段AE的三等分点时,求m的值;
②在平移过程中,是否存在以点A,N,E,M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由。
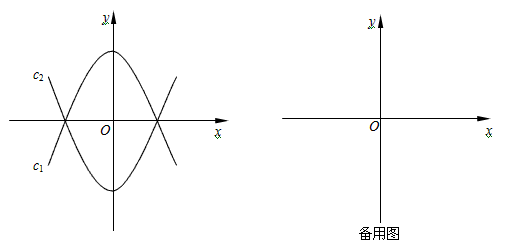
解:(1) ;
;
(2)①令 ,得:
,得: ,
,
则抛物线c1与x轴的两个交点坐标为(-1,0),(1,0),
∴A(-1-m,0),B(1-m,0),
同理可得:D(-1+m,0),E(1+m,0),
当 时,如图①,
时,如图①, ,
,
∴ ,
,
当 时,如图②,
时,如图②, ,
,
∴ ,
,
∴当 或2时,B,D是线段AE的三等分点;
或2时,B,D是线段AE的三等分点;
②存在,
理由:连接AN、NE、EM、MA,
依题意可得: ,
,
即M,N关于原点O对称,
∴ ,
,
∵ ,
,
∴A,E关于原点O对称,
∴ ,
,
∴四边形ANEM为平行四边形,
要使平行四边形ANEM为矩形,必需满足 ,
,
即 ,
,
∴ ,
,
∴当 时,以点A,N,E,M为顶点的四边形是矩形。
时,以点A,N,E,M为顶点的四边形是矩形。

 ;
;(2)①令
 ,得:
,得: ,
,则抛物线c1与x轴的两个交点坐标为(-1,0),(1,0),
∴A(-1-m,0),B(1-m,0),
同理可得:D(-1+m,0),E(1+m,0),
当
 时,如图①,
时,如图①, ,
, ∴
 ,
,当
 时,如图②,
时,如图②, ,
, ∴
 ,
,∴当
 或2时,B,D是线段AE的三等分点;
或2时,B,D是线段AE的三等分点; ②存在,
理由:连接AN、NE、EM、MA,
依题意可得:
 ,
,即M,N关于原点O对称,
∴
 ,
,∵
 ,
, ∴A,E关于原点O对称,
∴
 ,
, ∴四边形ANEM为平行四边形,
要使平行四边形ANEM为矩形,必需满足
 ,
,即
 ,
, ∴
 ,
,∴当
 时,以点A,N,E,M为顶点的四边形是矩形。
时,以点A,N,E,M为顶点的四边形是矩形。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 将抛物线c1:y=
将抛物线c1:y=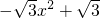 沿x轴翻折,得到抛物线c2,如图所示.
沿x轴翻折,得到抛物线c2,如图所示. 沿x轴翻折,得到抛物线c2,如图所示.
沿x轴翻折,得到抛物线c2,如图所示.
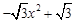 沿x轴翻折,得到抛物线c2,如图所示.
沿x轴翻折,得到抛物线c2,如图所示.