题目内容
如图，OA是⊙B的直径，OA=4，CD是⊙B的切线，D为切点，∠DOC=30°，则点C的坐标为________．
（6，0）
分析：连接BD，即可求得BC的长，进而求得OC的长，则坐标即可求得．
解答：
解：连接BD，
∵∠DOC=30°，
∴∠BDC=60°，
∴∠BCD=30°，
∴BC=2BD=4，
∴OC=OB+BC=6，
故点C的坐标为（6，0）．
故答案是：（6，0）．
点评：本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
分析：连接BD，即可求得BC的长，进而求得OC的长，则坐标即可求得．
解答：
解：连接BD，∵∠DOC=30°，
∴∠BDC=60°，
∴∠BCD=30°，
∴BC=2BD=4，
∴OC=OB+BC=6，
故点C的坐标为（6，0）．
故答案是：（6，0）．
点评：本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
相关题目
如图，火焰的光线穿过小孔O，在竖直的屏幕上形成倒立的实像，像的高度为1.5cm，OA=48cm，OC=16cm，则火焰的高度是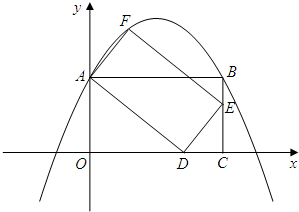
、n的代数式表示该抛物线；若不存在，请说明理由．
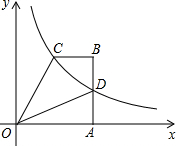直角梯形OABC中，BC∥OA，∠OAB=90°，OA=4，腰AB上有一点D，AD=2，四边形ODBC的面积为6，建立如图所示的直坐标系，反比例函数y=
如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-2，4），过点A作AB⊥y轴，垂足为B，连接OA．
)的半径；