��Ŀ����
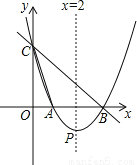
��ͼ��ֱ��y=��x+3��x�ᣬy��ֱ��ཻ�ڵ�B��C������B��C�����������y=ax2+bx+c��x�����һ����ΪA������ΪP���ҶԳ�����ֱ��x=2��
��1����������ߵĺ�������ʽ��
��2�����������������Ƿ���ڵ�Q��ʹ���Ե�B��C��QΪ�����������Ϊֱ�������Σ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
��3����S��0��4���Ķ�ֱ��l����������M��N���㣬�������������Ƿ���ڶ���T��ʹ�ò�������T������ֱ��l���С�MTN=90�㣿�����ڣ��������T�����ꣻ�������ڣ���˵�����ɣ�
��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ


 B.
B. 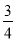 C.
C. 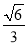 D.
D. 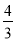
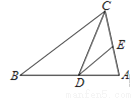
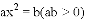 ���������ֱ���
���������ֱ���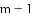
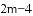
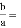 ________.
________.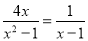
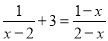 ��
��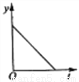 B.
B.  C.
C.  D.
D.